一種基于2FSK數字調制方式的Duffing混沌解調方法
摘 要:相干和非相干解調是2FSK數字通信中常用的方法,這兩種方法實現正確解調的前提是解調器的輸入信噪比不能太小,為了降低解調娶輸入信噪比,結合杜芬混沌系統所具有的較高檢測微弱周期信號的能力,提出杜芬系統解調2FSK數字信號的方法,但是由于傳統杜芬系統只適于檢測低頻信號,不能用于檢測高頻信號,因此建立了一種改進的杜芬系統,并將其運用到2FSK數字調制信號的解調過程中,Matlah仿真結果袁明,杜芬混沌接收系統可以有效地解調2FSK信號,另外,該系統還可以很好地抵制其他載波頻率信號的干擾.
關鍵詞:通信技術;2FSK數字調制;杜芬系統;解調:仿真
1 Sl 言 了混沌非相干解調系統。
在眾多的微弱信號檢測中,由于正弦信號的特殊性,使得正弦信號檢測理論和方法具有重要意義,特別在通信領域,正弦載波的檢測涉及到通信是否成功,因此具有極其重要作用。在通信系統設計中,總是希望在有效通信的情況下,盡量降低信噪比,這就要求接收系統具有檢測微弱周期信號的能力,在微弱正弦信號的檢測方面混沌系統占有重要地位,有關文獻[1—3]表明,杜芬(Duffing)系統對正弦信號檢測的信噪比達到了一】11 46 dB,然而目前時域方法處理信號的****信噪比門限只有一10 dB”,但是一般傳統的杜芬系統只檢測低頻正弦信號;
本文通過對系統的改進設計,提高了檢測頻率,并在此基礎上,采用杜芬系統對二進制數字調制的2FSK(二進制頻移鍵控)信號進行解調,建立2改進的Duffing混沌系統
Duffing系統”是在外部周期驅動力作用下產生混沌,其動力方程如下:
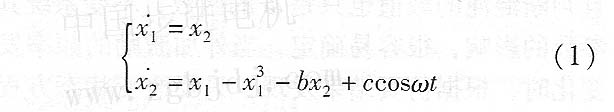 式中,c和m為外加周期驅動力的幅度、頻率;6 式中,c和m為外加周期驅動力的幅度、頻率;6
為阻尼比;z.。i為非線性恢復力。
根據文獻[7—9],當6=±1時,要求系統是混沌的,這種帶狀區域就是系統的混沌帶。
取b=1,m=1,C=0.8,系統在正弦信號驅動下產生的混沌相圖,如圖1所示。
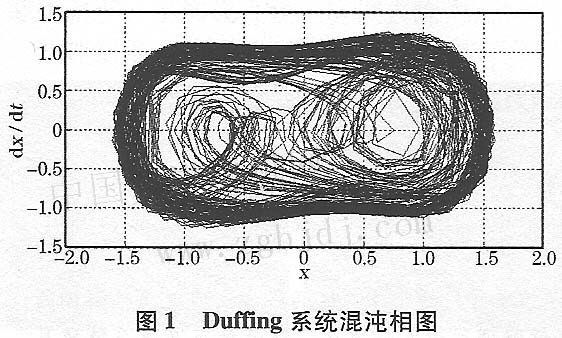
方程式(1)的Duffing系統只能檢測低頻的正弦信號,為了使方程式(1)適應檢測高頻正弦信號,并且保持混沌狀態不變,對式(1)的系統狀態方程作如下修改。
與式(1)對應的系統動力學方程為

條件可以看出,系統(7)中的參數對Harnilton方程及M6ln汰ov判斷方法沒有影響,并且判斷混沌的域值也只是m的函數,不受系統其他參數的影響,很容易確定,當外加激勵的頻率發生
變化時,根據仿真結果發現,只要改變狀態方程的系數m,就能產生混沌信號,并且該混沌系統所能檢測與激勵信號cos(m≠)同頻率的正弦信號。
外加與激勵信號cos(m)同頻正弦信號時混沌系統相圖,如圖2所示。
I
圖2大尺度周期圖
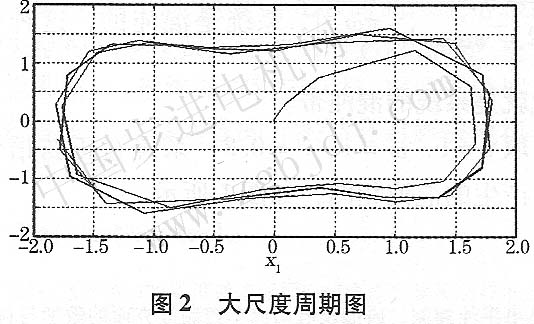
可以看出混沌系統狀態是大尺度周期的,其中,6=O.5,c:l,∞=100 000 md/s。根據文獻[9],分析式(2)~式(7)的推導過程,可以得出只,系統是混沌的,如果不加入外加信號,系統相圖與圖l是相似的,只是系統混沌狀態變化頻率遠大于圖l。
3 2FSK調制信號的Dung混沌接收解
調系統設計
由上文分析可以知道,Dumng混沌系統可以檢測正弦信號,當正弦信號加入Dumng混沌系統,系統是大尺度周期狀態,否則,系統是混 |