支持向量機(jī)理論及其在復(fù)雜電機(jī)設(shè)計中的應(yīng)用
(合肥工業(yè)大學(xué),安徽合肥230009)
摘要:闡述了支持向量機(jī)的歷史以及發(fā)展現(xiàn)狀,介紹了支持向量機(jī)在電機(jī)設(shè)計中的一些應(yīng)用。對其在永磁球形步進(jìn)電動機(jī)中的應(yīng)用前景進(jìn)行了展望。
0引 言
支持同量機(jī)(suppon vector mach jfle,以下簡稱svm)是at&t bell實驗室的v.vapnik提出的針對分類和回歸問題的統(tǒng)計學(xué)理論。它是由vapnik和其同事在1992年的計算學(xué)習(xí)理論(colt)會議上提出并介紹進(jìn)入機(jī)器學(xué)習(xí)領(lǐng)域,之后受到廣泛的關(guān)注。svm是機(jī)器學(xué)習(xí)領(lǐng)域若干標(biāo)準(zhǔn)技術(shù)的集成者。他集成了****間隔超平面、mercer核、凸二次規(guī)劃、稀疏解和松弛變量等多項技術(shù)。在若干挑戰(zhàn)性的應(yīng)用中,獲得了目前為止****的性能。在美國科學(xué)雜志上,支持向量機(jī)以及該學(xué)習(xí)方法被認(rèn)為是“機(jī)器學(xué)習(xí)領(lǐng)域非常流行的方法和成功的例子,并是一個令人矚目的發(fā)展方向。
svm是建立在統(tǒng)計學(xué)習(xí)理論和結(jié)構(gòu)風(fēng)險最小原理srm(structural risk minimization pnncidle)基礎(chǔ)上的,srm比傳統(tǒng)的基于經(jīng)驗風(fēng)險最小原理erm(empirical risk minmization pnciple)的神經(jīng)網(wǎng)絡(luò)方法具有明顯優(yōu)點。主要優(yōu)點有:(1)svm具有堅實的理論基礎(chǔ)和較好的推廣能力;(2)svm算法最終轉(zhuǎn)化為二次型尋優(yōu)問題,從理論上能夠得到全局****點;(3)svm具有強(qiáng)大的非線性處理能力和高維處理能力。基于這些優(yōu)點,svm在20世紀(jì)90年代中后期得到了全面深入的發(fā)展,現(xiàn)已成為機(jī)器學(xué)習(xí)和數(shù)據(jù)挖掘領(lǐng)域的標(biāo)準(zhǔn)工具。
本文對svm的歷史、發(fā)展現(xiàn)狀及基本理論進(jìn)行了概述,介紹了國內(nèi)外svm在電機(jī)中的一些應(yīng)用,最后,對svm在永磁球形步進(jìn)電動機(jī)中的應(yīng)用提出了自己的看法。
1支持向量機(jī)的提出和發(fā)展
1.1支持向量機(jī)的提出
1958年,rosenblatt****提出了一種學(xué)習(xí)機(jī)器的模型感知器,這標(biāo)志著對機(jī)器學(xué)習(xí)進(jìn)行數(shù)學(xué)研究的開始。之后隨著反向傳播(bp)技術(shù)的提出,機(jī)器學(xué)習(xí)的研究進(jìn)入了一個新的階段,即神經(jīng)網(wǎng)絡(luò)(neural nework)時代。在隨后的十幾年中,神經(jīng)網(wǎng)絡(luò)取得了很大的發(fā)展,并且在實際應(yīng)用中也取得了良好的效果。然而,神經(jīng)網(wǎng)絡(luò)存在著自身的局限性,其實現(xiàn)過程主要依賴于人的主觀意識和先驗知識,而不是建立在嚴(yán)格的數(shù)學(xué)理論基礎(chǔ)之上,岡此,對神經(jīng)網(wǎng)絡(luò)模型的性能及其適用范圍進(jìn)行理論分析就比較困難。另外,神經(jīng)網(wǎng)絡(luò)研究的是樣本數(shù)目趨于無窮大時的情況,但在實際問題中,樣本數(shù)目往往是有限的。因此,在實際應(yīng)用中很難取得理想的應(yīng)用效果。神經(jīng)網(wǎng)絡(luò)的過學(xué)習(xí)問題就是一個典型的例子。當(dāng)樣本數(shù)據(jù)有限時,本來具有良好學(xué)習(xí)能力的學(xué)習(xí)機(jī)器就表現(xiàn)出很差的泛化性能。
在這種背景下,vapnik等人從20世紀(jì)70年代開始致力于統(tǒng)計學(xué)習(xí)理論(statistical leamlng theory)方面的研究。統(tǒng)計學(xué)習(xí)理論(slt)是一種專門研究小樣本情況下機(jī)器學(xué)習(xí)規(guī)律的基本理論,為解決有限樣本學(xué)習(xí)問題提供了一個統(tǒng)一的框架,它將很多現(xiàn)有方法納入其中,有望幫助解決許多原來難以解決的問題。到90年代中期,隨著統(tǒng)計學(xué)習(xí)理論不斷發(fā)展和成熟,產(chǎn)生了基于統(tǒng)計學(xué)習(xí)理論基礎(chǔ)上的新的機(jī)器學(xué)習(xí)方法——支持向量機(jī)。它完全不同于神經(jīng)網(wǎng)絡(luò),神經(jīng)網(wǎng)絡(luò)算法是在模擬生物的基礎(chǔ)上構(gòu)造的,而svm算法的思想是來源于最小化錯誤率的理論界限。因此,svm算法具有良好的數(shù)學(xué)性質(zhì),如解的****性、小依賴輸入空間維數(shù)等等。svm所表現(xiàn)出種種優(yōu)良特性,使人們對這一新的機(jī)器學(xué)習(xí)算法開始重視,并已成為繼神經(jīng)網(wǎng)絡(luò)研究之后新的研究熱點。
1.2支持向量機(jī)的現(xiàn)狀
svm的提出引起了國內(nèi)外學(xué)者的高度關(guān)注,在短短幾年內(nèi),取得了一系列的研究成果。如:anthony等人提出了關(guān)于硬鄰域支持向量機(jī)學(xué)習(xí)誤差的嚴(yán)格理論界限,shawe-taylor和cristianini給出了軟鄰域支持向量機(jī)和回歸情況下的誤差界限;smola和schoelkodf提出了支持向量機(jī)一般意義下的損失函數(shù)數(shù)學(xué)描述;weston和vapnik等研究了支持向量機(jī)的泛化性能及其在多值分類和同歸問題的擴(kuò)展問題;脊回歸是由tikhonov提出的一種具有特殊形式的正則化網(wǎng)絡(luò),griosi、poggio等將其應(yīng)用到正則化網(wǎng)絡(luò)的學(xué)習(xí)中,而griosi、smola和schoelkopf等討論了正則化網(wǎng)絡(luò)和支持向量機(jī)的關(guān)系。目前,隨著支持向量機(jī)理論研究的不斷深入,出現(xiàn)了許多變種的支持向量機(jī),如sm01a提出的用于分類和回歸的v支持向量機(jī);mangasarian等人提出的通用支持向量機(jī)等。
2支持向量機(jī)原理
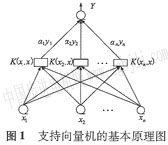
概況地說,svm就是通過某種事先選擇的非線性映射,將輸入向量映射到一個高維特征空間,在這個空問中構(gòu)造****分類超平面的實現(xiàn)過程。如圖l所示.
|