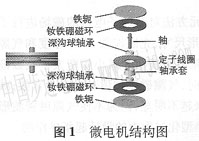
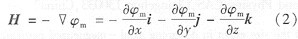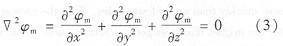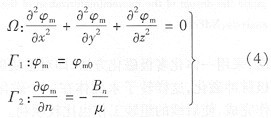軸向磁化永磁微電機(jī)轉(zhuǎn)子磁場(chǎng)分析
楊杰偉,蘇宇鋒,劉武發(fā),吳一輝
(1鄭州大學(xué),河南鄭州4500Ol;2中國(guó)科學(xué)院長(zhǎng)春光學(xué)精密機(jī)械與物理研究所,吉林長(zhǎng)春130033)
摘要:為研究尺寸效應(yīng)對(duì)軸向磁化永磁電機(jī)性能的影響,采用有限元方法對(duì)雙轉(zhuǎn)子電機(jī)的磁場(chǎng)進(jìn)行了仿真計(jì)算,得出了軸同磁化永磁電機(jī)轉(zhuǎn)子的氣隙磁密波形分布。分析了轉(zhuǎn)子外形尺寸、充磁極數(shù)、磁體厚度和氣隙長(zhǎng)度對(duì)氣隙磁密的影響,即隨著氣隙長(zhǎng)度的增加,充磁極數(shù)多的轉(zhuǎn)子產(chǎn)生的氣隙磁密幅值的減小幅度大于充磁極數(shù)少的;隨著磁體厚度的增加,氣隙磁密為一上升曲線,當(dāng)磁體厚度達(dá)到某一點(diǎn)時(shí),氣隙磁密幅值基本為一常數(shù);減小轉(zhuǎn)子直徑時(shí),隨著磁體厚度的降低,平均半徑處氣隙磁密幅值的減小幅度越來(lái)越不明顯,但為不使氣隙磁密波形變形嚴(yán)重,水磁轉(zhuǎn)子徑向長(zhǎng)度需至少大于1. 5 mm。分析結(jié)果可對(duì)該類電機(jī)微小型化過(guò)程中的設(shè)計(jì)起指導(dǎo)作用。
0引 言
近年來(lái),電子機(jī)械系統(tǒng)微小型化的發(fā)展日新月異,微電機(jī)作為微機(jī)電系統(tǒng)的關(guān)鍵部件,在電子機(jī)械系統(tǒng)中起主要作用。微電機(jī)微小型化將引起一系列性能的相應(yīng)變化,即隨著尺寸的減小,一方面,定子線圈微小型化,使線圈制作困難且安匝數(shù)下降;另一方面,電機(jī)的轉(zhuǎn)矩、功率和效率降低。制作永磁轉(zhuǎn)子的常規(guī)方法是,將較大的燒結(jié)磁塊切割成小磁體,對(duì)小磁體逐個(gè)進(jìn)行磁化,然后安裝定位于轉(zhuǎn)子鐵軛。在微電機(jī)微小型化過(guò)程中采用這種方法制作永磁轉(zhuǎn)子就很困難了,因?yàn)槲㈦姍C(jī)的微小型化必然促使永磁體向微小型化方向發(fā)展,這樣不但使永磁體充磁困難,而且由于磁體是在組裝之前被磁化的,對(duì)磁體的安裝定位也很不方便。為克服傳統(tǒng)方法的弊端,采用一體化多極磁化方法,即對(duì)整塊磁體進(jìn)行多極脈沖磁化,這樣轉(zhuǎn)子永磁體在一個(gè)磁化步內(nèi)即制作完成,使后續(xù)的組裝工作也比較順利。
微電機(jī)的磁性部件尺寸減小時(shí),它所產(chǎn)生的作為機(jī)電能量轉(zhuǎn)換媒介的氣隙磁場(chǎng)也相應(yīng)變化。在應(yīng)用領(lǐng)域中,微電機(jī)的主要性能指標(biāo)是輸出轉(zhuǎn)矩,而轉(zhuǎn)矩正比于永磁轉(zhuǎn)子在氣隙中產(chǎn)生的磁感應(yīng)強(qiáng)度,當(dāng)電機(jī)尺寸改變時(shí),加載電流后,轉(zhuǎn)矩也將隨之改變。因此轉(zhuǎn)子磁場(chǎng)分析對(duì)該類結(jié)構(gòu)電機(jī)的設(shè)計(jì)非常重要。軸向磁化永磁微電機(jī)定子線圈采用MEMs工藝光刻電鑄而成,為無(wú)槽結(jié)構(gòu),直接放置在軸向氣隙中,氣隙相對(duì)普通電機(jī)較大。
1轉(zhuǎn)子磁場(chǎng)有限元仿真分析
1.1微電機(jī)轉(zhuǎn)子的物理模型和數(shù)學(xué)模型
軸向磁化永磁微電機(jī)采用包括若干個(gè)平面線圈的定子和軸向磁化的燒結(jié)釹鐵硼雙轉(zhuǎn)子共同組成的三明治結(jié)構(gòu)(如圖l所示),轉(zhuǎn)子一體化多極軸向充磁,N、s交替成輻射狀均布于圓盤表面。電機(jī)中各部分磁密分布不均勻,不同半徑處的磁路長(zhǎng)度不相同,致使其磁場(chǎng)計(jì)算比普通圓柱式電機(jī)復(fù)雜。為了精確計(jì)算磁場(chǎng)分布,利用有限元軟件ANsYs電磁模塊對(duì)平面電機(jī)進(jìn)行電磁場(chǎng)仿真分析。
電機(jī)的空載磁場(chǎng)是靜磁場(chǎng),用標(biāo)量磁勢(shì)法進(jìn)行計(jì)算。麥克斯韋方程組是電磁場(chǎng)有限元分析的依據(jù)和出發(fā)點(diǎn),由麥克斯韋方程組可知,在穩(wěn)定磁場(chǎng)的無(wú)電流區(qū)域,磁場(chǎng)強(qiáng)度矢量的旋度為零,即:
引入標(biāo)量磁勢(shì)作為待求量
式中:φm為標(biāo)量磁勢(shì),H為磁場(chǎng)強(qiáng)度矢量。
將式(2)代人式(1),可導(dǎo)出標(biāo)量磁勢(shì)滿足的偏微分方程,即拉普拉斯方程:
將該泛定方程與邊界條件合在一起,構(gòu)成了邊值問(wèn)題,即穩(wěn)定磁場(chǎng)求解問(wèn)題的數(shù)學(xué)模型:
式中:Ω為求解區(qū)域,Г1為Dmchlet邊界條件,Г2為Neumann邊界條件,Bn為磁通密度矢量的法向分量,μ為磁導(dǎo)率。
l 2磁場(chǎng)計(jì)算結(jié)果
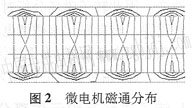
磁場(chǎng)計(jì)算結(jié)果表明,氣隙磁密的分布與半徑有關(guān)(圖2為平均半徑處周向展開(kāi)截面的通量線分布圖),在某個(gè)半徑處氣隙磁密分布近似為矩形波,在平均半徑附近氣隙磁 |