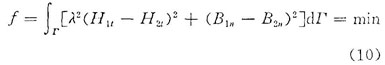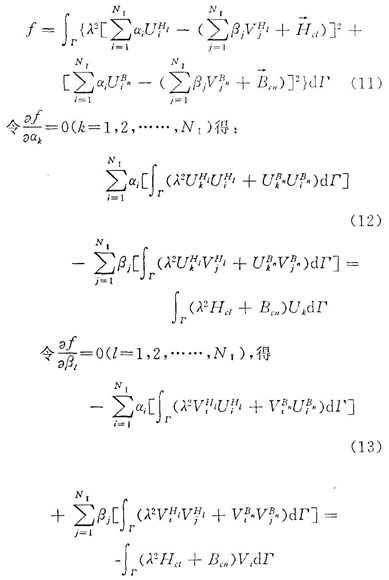新型等效源法計(jì)算含有鐵心的軸對(duì)稱(chēng)磁場(chǎng)
閏照文,趙玉清,陳德智,盛劍霓,王向暉
(西安交通大學(xué),陜西西安710049)
摘要:提出一種新型等效源法,該法中等效源的位置和個(gè)數(shù)可給以確定,由它產(chǎn)生的場(chǎng)分布可用級(jí)數(shù)表示,該方法克服了以前等效源的位置和個(gè)數(shù)只能憑經(jīng)驗(yàn)決定的缺點(diǎn),而成為一種科學(xué)的計(jì)算方法。用新型等效源法計(jì)算了含有鐵心的軸對(duì)稱(chēng)磁場(chǎng),結(jié)果表明,本方法比單獨(dú)用模擬磁荷法,既減少了等效源的個(gè)數(shù),又提高了計(jì)算精度。
關(guān)鍵詞:等效源;級(jí)數(shù)形式;邊界條件
l 引 言
等效源法(包括模擬電荷法、模擬磁荷法和模擬電流法)是電磁場(chǎng)數(shù)值分析中三種主要方法(有限元法、邊界元法和等效源法)之一,在電磁場(chǎng)數(shù)值計(jì)算中起到重要作用。但等效源的個(gè)數(shù)和位置都由經(jīng)驗(yàn)確定,這反映該方法缺乏科學(xué)性,難以保證計(jì)算精度,因此,這就大大限制了它的應(yīng)用范圍,本文提出的新型等效源法克服了上述缺點(diǎn)。
計(jì)算例子如圖1所示,求具有鐵心的圓柱線(xiàn)圈周?chē)拇艌?chǎng)分布,這場(chǎng)為一軸對(duì)稱(chēng)似恒磁場(chǎng)。用本文介紹的新型等效源法計(jì)算該模型,結(jié)果令人滿(mǎn)意,所需的內(nèi)存較邊界元法或有限元法少,但能滿(mǎn)足計(jì)算精度。
2新型等效源法
設(shè)鐵心為各向同性的線(xiàn)性均勻媒質(zhì),即μ1為常數(shù),將整個(gè)場(chǎng)域分為兩個(gè)區(qū)域,鐵心作為區(qū)域i,繞組所在空間作為區(qū)域ⅱ,見(jiàn)圖1。圖中a=o.01m,b=0.02m,a1=0.0105m,a2=0.0205m,線(xiàn)圈電流密度j=1.0×107a/m2,μl=2000,μ0。區(qū)域1中的標(biāo)量磁位φm1為全標(biāo)量位,滿(mǎn)足拉普拉斯方程:
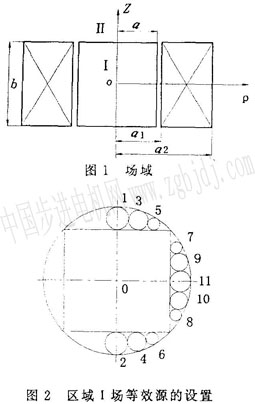
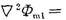 o,區(qū)域i中的標(biāo)量磁位為簡(jiǎn)化標(biāo)量位,也滿(mǎn)足拉普拉斯方程: 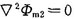 (實(shí)際場(chǎng)分布尚需加上由線(xiàn)圈激勵(lì)源產(chǎn)生的分量)。 求區(qū)域i中的場(chǎng)時(shí),等效源設(shè)置方法如圖2所示,0號(hào)、1號(hào)、2號(hào)均設(shè)置成球形等效源,o號(hào)源的表達(dá)式為:
1號(hào)、2號(hào)源的表達(dá)式為:
對(duì)于文中計(jì)算的軸對(duì)稱(chēng)場(chǎng),上式中的 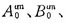 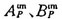 均為o。 3、4、5、6、7、8、9、10、11號(hào)等效源為環(huán),作用中心在環(huán)的中心線(xiàn)上,其表達(dá)式為:
式中k為第一類(lèi)完全橢圓積分,qi為待求常數(shù)。
求區(qū)域i中的場(chǎng)時(shí),等效源設(shè)置方法如圖3所示,o號(hào)等效源設(shè)置成球形等效源,表達(dá)式為:
1’、2’、3’、4’、5’、6’號(hào)等效源為環(huán),其作用中心也在環(huán)的中心線(xiàn)上,表達(dá)式為:
3用最小二乘法確定待定常數(shù)
得到了區(qū)域i、ⅱ的磁位表達(dá)式后,即可求出兩個(gè)區(qū)域內(nèi)的場(chǎng)量表示式,分別為:
區(qū)域i:
式中 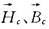 為圓柱線(xiàn)圈產(chǎn)生的場(chǎng)分量,可山畢奧一沙伐定理計(jì)算。 取目標(biāo)函數(shù)
式中λ為加權(quán)系數(shù)。
把(6)、(7)、(8)、(9)式代入(10)式有
上式中取n1=31,其中級(jí)數(shù)項(xiàng)系數(shù)為22,環(huán)咀荷數(shù)為9個(gè);取n1=28,其中級(jí)數(shù)項(xiàng)系數(shù)為22,環(huán)電荷數(shù)為6個(gè)。
表示成矩陣形式有:
|



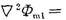 o,區(qū)域i中的標(biāo)量磁位為簡(jiǎn)化標(biāo)量位,也滿(mǎn)足拉普拉斯方程:
o,區(qū)域i中的標(biāo)量磁位為簡(jiǎn)化標(biāo)量位,也滿(mǎn)足拉普拉斯方程: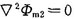 (實(shí)際場(chǎng)分布尚需加上由線(xiàn)圈激勵(lì)源產(chǎn)生的分量)。
(實(shí)際場(chǎng)分布尚需加上由線(xiàn)圈激勵(lì)源產(chǎn)生的分量)。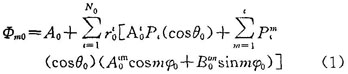
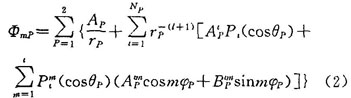
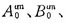
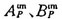 均為o。
均為o。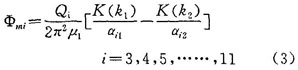

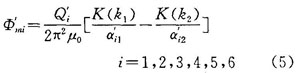
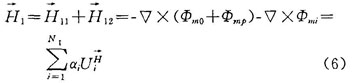
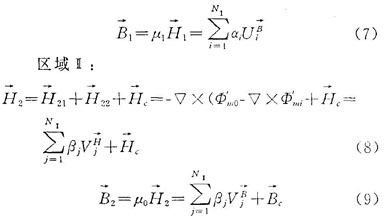
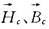 為圓柱線(xiàn)圈產(chǎn)生的場(chǎng)分量,可山畢奧一沙伐定理計(jì)算。
為圓柱線(xiàn)圈產(chǎn)生的場(chǎng)分量,可山畢奧一沙伐定理計(jì)算。