磁阻式步進電動機靜態轉矩特性的數值分析
鄒景祥 高 巖 (上海工業大學)
【摘 要】采用確限元數值解法、網格自動剖分技術對磁阻式步進電動機在半個齒距范圍內進行了磁場分析,分別計算了磁阻式步進電動機單相通電和雙相通電時的靜態轉矩性,計算結果與實測值甚為接近,達到了工程設計要求。
【敘 詞】步進電動機磁阻電動機靜態特性轉矩有限無法數值計算優化設計
1 引 言
步進電動機的設計和優化設計中最重要的是性能指標的預測,但是由于步進電動機的結構和運行條件特殊,人們在計算過程中往往要作某些假設,例如忽略磁路的飽和或是假定鐵心部分的磁壓降與轉子位置無關等,以求得到簡化,這自然會給計算結果帶來一定的誤差。為了充分考慮電機磁路的飽和對其性能的影響,本文將以樣機bf36型磁阻式步進電動機為例,采用有限元數值解法,并借助網格自動剖分技術,對整個電機的求解區域進行磁場分析,求得電機磁場的磁共能,進而計算出電機的靜態轉矩。磁阻式步進電動機的定、轉子齒形尺寸的不同,將影響電機磁路的磁導和電機磁場,從而影響電機的性能。
2靜態轉矩特性的有限元數值計算
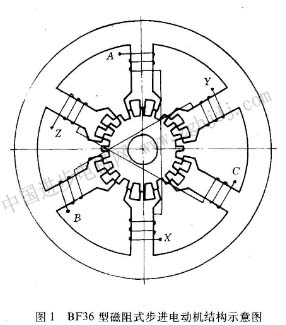
bf36型三相磁阻式步進電動機的結構如圖1所示,定子上共有6個磁極,每極上有3個矩形齒,轄子上有zr=20個均勻分布的矩形齒,定轉子齒矩盧18度。電機的un= 24v,ln= 0.15a,可以單相通電,也可以雙相通電運行。
用有、限元數值解法計算磁阻式步進電動機的靜轉矩。可直接利用電機磁場的磁共能計算電磁轉矩的公式[1]。
式中θr一轉子的角位移,radθ一轉子的角位移,
為了算出電機的靜態轉矩特性,即矩角特性,就必須研究電機定子磁極線圈在不同電流下,以及轉子相對定子有不同位置時的磁場分布情況。由于在齒距t范圍內,在 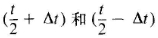 的位置電機磁場對稱,故只需研究半個齒距,即9度范圍內各個位置的磁場情況即可。 設定轉子齒中心線對齊時θ=0,根據電機的結構、+通電方式和磁場對稱性,可選定半個電機的空間作為電機磁場的求解區域,圖2示出這時求解區的網格剖分。
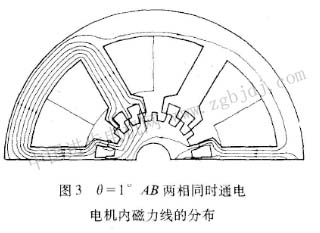
在某一θ值下磁極線圈通入電流后,經二維磁場的有限元計算[2]可得出此時求解區域內部節點的矢量磁位a值、各單元的磁通密度以及繪出求解區的磁力線分布。圖3展示了θ=1度時,a、b兩相同時通電的磁力線分布,再經后處理的計算,便可求得通電的磁極線圈所匝鏈的總磁鏈ψ。然后,改變電流的數值,再計算該θ位置的磁場和磁極線圈匝鏈的總磁鏈新值。這樣,重復多次計算后便可得到一組不同的電流及其所產生的磁極線圈磁鏈,即得出在此轉子位置θ下電機的電流與線圈磁鏈之間的關系ψ=f(i).
如果轉子在空間從θ=0起按順時針方向每轉過1度,再重復上述計算,直至θ=9度止(這在有限元數值分析中借助網格自動剖分技術后是容易實現的),從而得出電機在所有10個定、轉子相對位置的磁鏈與電流間的關系。圖4是a相繞組通電狀態下θ=0和θ=1度時電機的ψ=f(i)關系曲線。從而可用simpson積分法‘3’分別求出在某一電流下各個θ位置的磁共能遍wm,例如i= in=0.15a,θ=0時的磁共能值就是曲邊形oaco的面積,θ=1度時的磁共能則為曲邊形obco的面積。重復上述步驟,便可求出在此電流下θ=0.1度.2度……9度時所對應的10個電規的磁共能,即有wm對應于0的10組對應值。然后,再用三次樣條插值函數的微分公式(4)就能求得磁共能wm。對θ導數,并根據式(i)即可得出步進電動機的靜轉矩特性曲線t=f(θ)。圖5和圖6表示該電機在額定電流下單相通電和兩相同時通電時計算所得的靜轉矩特性。圖7和圖8則分別表示所對應的實測結果。兩者相比較,****靜轉矩的誤差在單相通電時是百分之5 .41,兩相同時通電時為百分之7.34。
< |




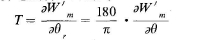
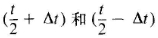 的位置電機磁場對稱,故只需研究半個齒距,即9度范圍內各個位置的磁場情況即可。
的位置電機磁場對稱,故只需研究半個齒距,即9度范圍內各個位置的磁場情況即可。