磁懸浮控制系統的狀態空間設計
李莎1,許賢澤2
(1湖北第二師范學院,湖北武漢430205;2武漢大學,湖北武漢430079)
摘要:介紹了單電磁鐵懸浮系統的動態模型,并以該動態模型為基礎,采用狀態空間法設計了以電壓作為輸入控制量的閉環控制器,并且運用Maflab進行了相應的仿真。該方法簡單實用,控制參數無需經驗試湊。試驗結果表明,系統控制效果良好,有一定的實用價值。
關鍵詞:磁懸浮系統;非線性;狀態空間法;極點配置
中圖分類號:TM301.2 文獻標識碼:A 文章編號:1004—7018(2008)06—0010—03
磁懸浮系統是一個復雜的非線性系統,傳統的系統控制器常采用基于傳遞函數模型的設計法(如HD設計法[1,2]),在設計過程中,其主要控制參數往往需要憑經驗試湊;而狀態空間設計法是一類以系統狀態空間模型(即狀態空間表示式)為基礎的分析設計方法,基本上不需要憑經驗試湊。
1磁懸浮系統的狀態方程
磁懸浮系統一般由多個電磁鐵組成,而其中每個電磁鐵的動態模型一般是相同的。圖1為單個電
磁鐵與金屬導軌組成的懸浮系統工作原理圖。圖中,mg為電磁鐵重力,fd為外界擾動量,F(i,t)為電磁吸力,z(t)為磁極表面相對參考平面的距離,h(t)為導軌表面相對參考平面的距離,c(t)為磁極與導軌問的氣隙,i(t)為控制線圈電流,u(t)為繞組回路的電壓。
取重力方向為正方向,選擇(△c,△c,△i)T作為狀態變量,并對系統進行平衡點(i。,c。)附近線性化處理,可得以下狀態方程(忽略鐵心和導軌中的磁阻以及繞組漏磁通):
鐵磁極面積,N是電磁鐵線圈匝數。
可見,此系統是一個三階開環系統。通過勞斯(Rol-th)判據可知,它具有不穩定性。因此,為了保證電磁鐵能夠穩定懸浮,需要給這個系統加一個反饋控制。
2狀態空間設計法
狀態空間設計法是通過狀態反饋控制系統狀態行為來實現控制目標的。其著眼點是系統的內部特性和系統狀態的行為。其設計任務是確定控制目標和求解可實現控制目標的狀態反饋控制律[3]。采用此設計方法需有一個前提,即系統必須具有能控性和能觀性。
2.1系統的能控性和能觀性
系統的能控性和能觀性都是系統的一種內在特性,分別反映系統控制作用和輸出量與系統狀態之間的特征關系,它們都是由系統本身結構和參數所決定的。忽略式(1)中的軌道形變△h(t)和動態干擾fd(t),可得該方程的系數矩陣:
通過式(2)、式(3)可知,系統的能控陣和能觀陣的秩均為3,故系統既可控又可觀。
2.2系統的極點配置
既然系統是完全能控的,則配置系統的閉環極點,可以使得原來不穩定的受控對象變為閉環穩定。由式(1)可知,以電壓為輸入控制的磁懸浮線性化系統是一個三階系統 [4]。于是選擇一對主導極點為: 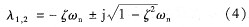 式中:ζ和ωn分別是二階系統的阻尼系數和無阻尼自振角頻率。將另一個極點定于主導極點左邊較遠的地方,使得該極點對閉環系統的動態性能影響很小。這樣就可以把系統看成是只有主導極點的二階系統。
設閉環系統滿足以下動態指標:輸出超調量σ≤百分之2.O,調整時間ts≤O.10s。二階模型的超調量和調整時間近似計算公式:
取ζ=0.80,ωn=52,代人式(4)可得主導極點為λl,2=-41.6±j31.2,再選擇極點λ3,為十倍遠,即λ3=-500,則系統期望的閉環特征多項式為:
3系統控制器的設計與仿真
引入狀態反饋控制律:
式中:s表示在復平面中展開,I為單位矩陣。
為使此系統達到前述的極點配置要求,將式(7)對照式(5)可得:
根據式(6),并代入各項參數,可得此系統的simulink仿真結構圖,如圖2所示。
給定軌道氣隙噪聲csrc大小為5 mm,頻率為1Hz,可以仿真得出系統氣隙響應和電流變化曲線,如圖3所示。 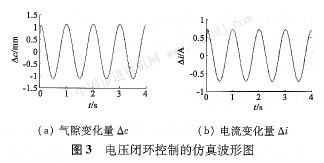 分析仿真波形圖3可知,當氣隙噪聲為1 Hz、5mm時,該控制器能夠將氣隙變化量控制在大約±1.1 mm以內,且此時電流波動大約為±0.7 A。
4結語
本文在單電磁鐵懸浮系統的動態模型的基礎上,設計了一種基于狀態空間法的電壓閉環控制器,并通過Matlah對控制器的性能進行了仿真。實驗結果表明該控制器能夠較好地實現磁懸浮的穩定控制。由于磁懸浮系統需要實時控制,因此在硬件設計方面應考慮采用具有高速運算能力的控制器(如DsP[5,6,7]),并且在電路設計中必須十分重視抗干擾
問題。
|