Halbach型永磁陣列的磁場分析
周 贛,黃學良,沈 妍,周勤博
(東南大學,江蘇南京210096)
摘 要:以平面電機課題中采用的Halbach陣列為例,采用一種永磁陣列的通用分析方法對磁場進行了解析計算和諧波分析,利用ANSYS對徑向和Halbach陣列的磁場進行了仿真和比較,最后用MATLAB對ANSYS的磁場仿真結果進行了諧波分析。計算和仿真結果表明,Halbach陣列具有磁單邊特性,且磁場在強側具有優良的正弦特性。
關鍵詞:Halbach陣列;諧波分析;仿真
中圖分類號:TMl53 文獻標識碼:A 文章編號:1004-7018(2008)07—0001一03

0 引 言
Halbach永磁陣列的概念最早是由美國勞倫斯伯克利國家實驗室的K1aus Halbach教授提出[1],并在20世紀90年代被國內外研究機構相繼成功應用于新一代的粒子加速器、自由電子激光裝置、同步輻射裝置等高能物理領域中。
Halbach陣列是一種新型永磁體排列方式,它將不同磁化方向的永磁體按照一定的順序排列,使得陣列一邊的磁場顯著增強而另一邊顯著減弱,且很容易得到在空間較理想正弦分布的磁場。Halbach陣列的這些特性使其在永磁電機領域中具有廣闊的應用前景,Halbach陣列在學術界和工業界都受到了廣泛的關注。近十幾年來,在權威期刊和國際會議上,有很多與Halbach陣列相關的文獻出現。有些知名大學(如MIT、東京大學)已經對Hal—bach陣列的應用進行了卓有成效的研究口[2,3]。
本課題組目前正在開展基于Halbach陣列的高精度平面電機的研究,即在設計和制造出平面Hal—bach磁陣列的基礎之上,研制一套高精度平面電機系統。研究的第一步就是在電磁理論指導下設計不同拓撲結構的Halbach永磁陣列,并通過解析和仿真的手段來分析陣列的特性。
參考國內外高精度平面電機的結構,課題組最終選擇永磁直線電機作為執行器,直線電機的永磁陣列采用一維Halbach陣列。本文中,首先對Halbach陣列的磁場進行了解析求解,并對磁場進行了諧波分析,利用ANSYS和MATLAB軟件對陣列磁場進行了仿真分析,仿真結果進一步驗證了Halbach陣列的優良特性。
1 Halbach陣列的解析分析方法
MIT的Kim博士在文獻[2]中提出了一種永磁陣列的通用解析算法。下文首先介紹該算法,接著利用它來分析如圖1所示的陣列。
圖2為傅立葉級數表示的永磁陣列的二維模型,其中△高度的陰影區域代表永磁陣列,空白區域為自由空間;永磁陣列的磁化強度沿Z軸周期分布。(周期為L),第n次諧波的空間角頻率為k n = 2nπ/L (另外定義 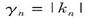 ); 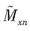 和 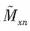 為磁化強度的傅立葉系數;假設陣列沿y軸的無限延伸a,b,c,d表示磁陣列的邊界。 對圖2所示的永磁陣列,可推導出[2]
式(1)為圖2的永磁陣列x方向磁感應強度的傅立葉系數求解公式,式(2)為z方向磁感應強度的傅立葉系數求解公式。
圖3為圖l陣列的二維拓撲結構,其中每對磁極由四段磁體構成,空間周期L=25.4 mm,陣列厚度 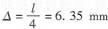 。永磁體采用釹鐵硼材料,剩磁B r=1.3 T。
下文將用已介紹的永磁陣列的通用計算方法來
分析圖3陣列的磁場。
當采用圖3的坐標系統時,陣列的磁化強度分布情況如圖4所示。根據傅立葉級數的定義: 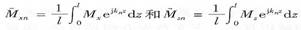 可推導出磁化強度的傅立葉系數為:
遞增n,把式(3)和式(4)代入式(1),并代人x=△和x=0,可計算出邊界a和d處x方向上的磁感應強度的諧波,計算結果如圖5所示(因z方向磁場特性和x方向類似,下文分析都以x方向磁場為例)。
用類似的方法可計算出x=-0.25mm 和 x=-1mm出場的各次諧波的比例并用餅圖的形式表示,如圖6所示。
通過以上計算和分析,得到了Halbach陣列的若干重要特性:
(1)若定義x≤O區域為強側,x≥△區域為弱側。計算結果表明:強側磁場基波幅值為0.94 T,弱側磁場不存在基波分量,其幅值****的3次諧波幅值為0.38 T,磁場呈現明顯的單邊性。
(2)從圖5可以看出,強側磁場只含有基波、5次諧波、9次諧波等諧波分量,而不包含3次、7次、11次等諧波分量,這說明較傳統陣列,Halbach陣列磁場在強側具有更好的正弦特性:
(3)從圖6可以看出,基波比例隨氣隙增大迅速增大,各高次諧波比例則迅速減小。在邊界d處,各高次諧波占46%之多;當氣隙增大為0.25 mm時,高次諧波含量下降為29%;而在l mm氣隙處,基波含量為92%,5次諧波含量為8%,其余高次諧波則基本衰減為O,在該氣隙高度就可得到較為理想的正弦磁場。
上述分析表明,Hdbach陣列的磁場在強側具有優良的正弦特性,且高次諧波幅值隨氣隙的增大迅速減小。即使采用簡單繞組和非斜槽結構,H albach電機也可以得到理想的正弦分布磁場,這大大降低了電機的制造成本并簡化了工藝。
2 HaIbach陣列有限元仿真分析
圖7為傳統電機中經常采用的徑向磁化陣列,設它和圖3的Halbach陣列具有相同的體積。在ANsYs中建立圖3和圖7陣列的二維模型并進行磁場仿真,磁力線分布的仿真結果如圖8所示。
整理和對比兩種陣列的仿真結果數據可以得到
如下結論:
(1)從圖8可以看出,徑向陣列磁場具有對稱性,Halbach陣列磁場呈現單邊性,強側磁場明顯強于弱側磁場。
(2)在強側O.25 mm氣隙處,Halbach陣列磁感應強度幅值為0.863 l T,徑向陣列在0 25 mm氣隙處磁感應強度幅值為0.569 2 T,Halbach陣列磁場幅值為徑向陣列磁場的1.5倍左右。
磁場仿真結果表明:Halbach陣列具有明顯的磁單極子特性。研究表明,在無背鐵引導磁路的情況下,H albach陣列也可在強側形成足夠大的磁場,這樣不僅可以減少電機重量以得到優良的動態特性,而且還可以減少鐵耗,大大增加電機的效率;另外弱側磁場很小的特性也使得Halbach陣列被應用在需要進行磁屏蔽的場合(例如磁懸浮列車)。
(1)提取500個點的磁場數值,作為原始曲線的離散函數值輸入到MATLAB里。
(2)設擬合函數為y=且sln(Bx+c),MATLAB求出的具有最小擬合誤差函數為:y=0.8398×sin(245 .1+0.8175)。因只用一個正弦函數來擬合原始曲線,該正弦函數可近似作為原始曲線的基波分量,擬合結果如圖10所示.
(3)為求出影響****的高次諧波分量,可設置擬合曲線形式為:Y=A1sin(B1z+C1)+A2sin(B2z+C。),MATLAB求出的具有最小擬合誤差的函數為:Y=0 84sin(246.5x+0.7974)+0.07313sin(1235x+0.7955),擬合結果如圖11所示。直觀來看,圖11的擬合曲線較圖10的擬合曲線更加接近原始益線。假設基波為0.84sin(246.5x+0.7974),基波角頻率為246 5,函數0.07313sin(1235x+0.7955)的角頻率為1235,由1235+246.5—5可知,其為5次諧波。
(4)上述方法可用于求解磁場的更高次諧波,但由于更高次諧波的幅值很小,利用該方法計算誤差就會較大,所以在這里就不繼續往下分析。
上述分析說明,5次諧波對Halbaeh陣列強側磁場的影響****。
4結語
以平面電機課題中采用的Halbach陣列為例,作者首先利用一種永磁陣列的通用分析方法對磁場進行了解析計算和諧波分析,接著利用ANsYs對徑向和Hdbach陣列的磁場進行了仿真和比較,最后利用MATLAB對ANsYs的仿真結果進行了諧波分析。計算和仿真結果表明,H aJbach陣列具有磁單極子特性,且磁場在強側具有優良的正弦特性,這些特性已被廣泛應用在各種電機領域中[4].
|