一種實(shí)時修正解耦參數(shù)的優(yōu)化矢量控制方法
李皎潔,蘇中義,張向鋒
(上海電機(jī)學(xué)院,上海200240)
摘要:提出了一種實(shí)時修正感應(yīng)電動機(jī)矢量控制中解耦參數(shù)的方法。在矢量控制的電壓解耦計(jì)算中增加了參數(shù)修正計(jì)算,通過可測量的參數(shù)值推導(dǎo)解耦電壓參數(shù),并實(shí)時更新,矢量控制的解耦參數(shù)能跟隨電動機(jī)實(shí)際運(yùn)行參數(shù)的變化,提高了解耦的效用。仿真結(jié)果表明該方法是有效的。
關(guān)鍵詞:矢量控制;感應(yīng)電動機(jī);交叉解耦;參數(shù)修正
中圖分類號:TM346 文獻(xiàn)標(biāo)識碼:A 文章編號:1004—7018(2008)05—0046—03
0引言
感應(yīng)電動機(jī)的電流、電壓、磁通和電磁轉(zhuǎn)矩等變量存在復(fù)雜的耦合關(guān)系。針對這個問題,許多矢量控制策略被提出,但是它們在應(yīng)用中都不可避免地存在電機(jī)參數(shù)敏感性以及噪聲抑制等問題[6]。眾多的矢量控制策略中以基于轉(zhuǎn)子磁場定向構(gòu)成的控制系統(tǒng)最為常見,它的可控電壓模式不僅易于實(shí)現(xiàn)解耦,而且控制結(jié)構(gòu)大大簡化。在基于轉(zhuǎn)子磁場定向的矢量控制的解耦計(jì)算中,解耦項(xiàng)的參數(shù)往往是恒定值,但是實(shí)際環(huán)境下的電機(jī)參數(shù)敏感變化,導(dǎo)致定子電流的勵磁分量和轉(zhuǎn)矩分量的耦合不能****消除,降低了系統(tǒng)性能。
針對這個問題,本文提出一種優(yōu)化矢量控制方法,根據(jù)可測量的參數(shù)值推算解耦電壓。通過實(shí)時修正解耦參數(shù),使得解耦計(jì)算符合當(dāng)前的電機(jī)運(yùn)行狀態(tài),實(shí)現(xiàn)交叉耦合的完全解耦,降低參數(shù)敏感對控制性能的影響。最后本文通過對控制過程的仿真驗(yàn)證了該方法的有效性。
1感應(yīng)電動機(jī)等效模型
M-T同步旋轉(zhuǎn)坐標(biāo)系下,感應(yīng)電動機(jī)的數(shù)學(xué)模型[1]可描述為:
式中:ω1為定子磁場旋轉(zhuǎn)速度,ωs為轉(zhuǎn)差角速度,P為感應(yīng)電動機(jī)極對數(shù),Ψ2為轉(zhuǎn)子磁鏈。
考慮到電動機(jī)運(yùn)行時動態(tài)性能的討論,引入電機(jī)拖動公式:
式中:σ為定子瞬間電感系數(shù), 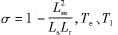 分別為電磁轉(zhuǎn)矩和負(fù)載轉(zhuǎn)矩,P為極對數(shù),J為轉(zhuǎn)動慣量,可得M-T同步旋轉(zhuǎn)坐標(biāo)系下感應(yīng)電動機(jī)的等效模型結(jié)構(gòu),如圖l所示。 2解耦參數(shù)的實(shí)時修正方法
由圖1可見,決定轉(zhuǎn)子磁鏈Ψ2穩(wěn)態(tài)值的勵磁電流分量iM1和決定電磁轉(zhuǎn)矩Te穩(wěn)態(tài)值的轉(zhuǎn)矩電流分量iT1之間存在交叉耦合,需要解耦.針對這個問題,前人提出了很多種交叉耦合的解耦算法,如對角矩陣解耦法、單位矩陣解耦法、前饋控制解耦法,反饋控制解耦法等,這些方法在參數(shù)不變的情況下都能十分有效地解耦。但是電機(jī)運(yùn)行時其參數(shù)不斷變化,導(dǎo)致解耦算法產(chǎn)生偏差,電機(jī)的控制性能也受到影響。
反饋解耦算法是矢量控制交叉解耦中常見的解耦算法,它將感應(yīng)電動機(jī)的M、T軸電流的反饋量用于電動機(jī)解耦電壓的計(jì)算,并將其引入電機(jī)控制電壓輸入端進(jìn)行疊加補(bǔ)償。這種解耦算法是建立在定子電流反饋量無延遲,和交叉耦合項(xiàng)中的電機(jī)自感系數(shù)Ls、漏感系數(shù)σ的計(jì)算估算值和實(shí)際值高度吻合基礎(chǔ)上的。當(dāng)電機(jī)參數(shù)改變或者運(yùn)行頻率改變時,解耦電壓的計(jì)算值與實(shí)際值之間分別存在偏差 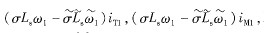 不可能達(dá)到完全解耦[7]。本文以反饋解耦法為例,提出實(shí)時計(jì)算等效解耦參數(shù)的方法,反饋解耦法的結(jié)構(gòu)如圖2所示。 則式(7)就是解耦項(xiàng)修正公式,根據(jù)這個公式可由電機(jī)測量參數(shù)推導(dǎo)交叉耦合項(xiàng)的值,在解耦算法中應(yīng)用該值,實(shí)時修正交叉解耦項(xiàng)的大小,則可保證解耦電壓總是與實(shí)際運(yùn)行參數(shù)匹配。將式(7)中的ω1Lsσ一代人反饋電壓解耦算法中,得實(shí)時解耦控制電壓公式為:
式中:uM1、uT1、iM1、i1是當(dāng)前運(yùn)行時的M、T軸的電壓電流值,可通過將定子端可測量所得相電壓、相電流矢量變換,折算到M-T軸坐標(biāo)下獲得。把折算量代人式(7),即得在當(dāng)前電機(jī)參數(shù)下的交叉解耦項(xiàng)ω1Lsσ,代人式(9)、式(10)得當(dāng)前解耦控制電壓值,用于新一輪控制輸入。
3仿真和實(shí)驗(yàn)結(jié)果
感應(yīng)電動機(jī)矢量控制方法的仿真框圖如圖3所示。異步電動機(jī)三相電壓值、電流值和實(shí)際轉(zhuǎn)速值為測量參數(shù),轉(zhuǎn)速設(shè)定和轉(zhuǎn)子磁鏈為給定值。
仿真初始值設(shè)定如下:異步電動機(jī)三相電壓、電流初始值分別設(shè)為220 v、3.8 A,實(shí)際轉(zhuǎn)速初始值為0,給定轉(zhuǎn)子磁鏈蝣初始值設(shè)為0.05 H,給定轉(zhuǎn)速ω初始值為314rad/s。
運(yùn)行過程中電動機(jī)參數(shù)的變化是漸變的,但是為了方便對比參數(shù)變化前后的不同,我們采用參數(shù)突變方式執(zhí)行仿真,使仿真結(jié)果更能突出參數(shù)實(shí)時修正方法的作用。感應(yīng)電動機(jī)仿真參數(shù)如表1所示。  采用常規(guī)反饋解耦計(jì)算的矢量控制算法進(jìn)行仿真,得出反饋解耦方法的等效電流iM1、iT1響應(yīng)曲線如圖4中虛線所示;采用實(shí)時修正反饋解耦參數(shù)的矢量控制算法進(jìn)行仿真,得出反饋解耦法的等效電流iM1、iT1響應(yīng)曲線如圖4、圖5中實(shí)線所示。
對比響應(yīng)曲線可以看出,在變頻調(diào)速中,當(dāng)電動機(jī)參數(shù)發(fā)生改變,或者頻率改變導(dǎo)致電機(jī)中同步轉(zhuǎn)速ω1的值改變時,如果解耦環(huán)節(jié)中的解耦電壓仍使用固定的參數(shù)計(jì)算,矢量控制iM1、iT1的解耦會受到影響。當(dāng)采用實(shí)時修正解耦參數(shù)計(jì)算以后,在變頻以及電機(jī)運(yùn)行參數(shù)變化過程中實(shí)現(xiàn)了動態(tài)匹配,其解耦效果基本不受參數(shù)變化或頻率變化的影響,進(jìn)一步優(yōu)化了iM1、iT1的獨(dú)立,勵磁分量和轉(zhuǎn)矩分量的相互影響進(jìn)一步降低。
4結(jié)語
本文針對矢量控制中交叉解耦受電機(jī)參數(shù)變化影響的問題,優(yōu)化了解耦計(jì)算環(huán)節(jié),在常規(guī)解耦計(jì)算中加入實(shí)時參數(shù)修正計(jì)算,使解耦項(xiàng)符合電機(jī)實(shí)際運(yùn)行參數(shù),該方法極好地消除了參數(shù)變化對矢量控制精度的影響。通過仿真證實(shí),在反饋解耦法中應(yīng)用修正計(jì)算后,交叉解耦不受電機(jī)參數(shù)變化影響,解決了解耦中的參數(shù)敏感問題。
本文的創(chuàng)新點(diǎn)是:采用可實(shí)時測量的參數(shù)推算交叉解耦項(xiàng),進(jìn)一步推算解耦電壓,通過實(shí)時計(jì)算更新,保證解耦過程不受電機(jī)參數(shù)變化影響。
|