PMSM定子鐵耗與磁極渦流損耗計算及其對溫度場的影響
張洪亮,鄒繼斌,陳霞,江善林
(哈爾濱工業大學,黑龍江哈爾濱150001)
摘要:采用二維有限元法對交流水磁同步電動機(PMsM)定子與磁極區域電磁場進行了分析研究,闡述了定子鐵心不同區域磁場的變化規律以及磁極區域渦流場的分布規律:在此基礎上,綜合考慮電機中交變與旋轉磁場的影響,計算了電機定子飽和鐵心損耗與磁極渦流損耗,并將此計算結果應用于電機的三維溫度場計算中,分析了兩類損耗對電機溫升的影響。通過計算結果與實測值的對比分析,驗證了損耗與溫度場計算方法的正確性。
關鍵詞:水磁同步電動機;鐵耗;渦流損耗;溫度場
中圖分類號:TM341 文獻標識碼:A 文章編號:1004一7018(2008)05—0001—04
O引 言
永磁同步電動機(以下簡稱PMsM)具有效率高、功率密度高、控制性能好等優點,廣泛應用于高性能的驅動領域。PMsM鐵心中的磁場變化規律比較復雜,與電機的結構、轉速及控制策略密切相關,此外,電機正常工作時,定子鐵心中的磁通密度是非正弦、非線性的,且各處的磁通密度不同,而鐵心損耗又與磁通密度幅值呈非線性關系,對于此類飽和鐵心損耗的計算是比較困難的。傳統上認為鐵心內磁場只發生交變,僅產生交變鐵心損耗,而實際上一部分鐵心處于旋轉磁場中,也產生旋轉鐵心損耗,因此為了準確定量計算飽和鐵心損耗,首先確定鐵心內任意點的磁密變化規律是必需的。
鐵耗在整個電機損耗中占有重要地位,也是引起電機發熱的主要原因之一。一般對表面磁鋼式永磁同步電動機的研究認為,該電機氣隙大,且磁鋼的磁導率近似為空氣的磁導率,電樞反應很小,且轉子以同步轉速旋轉,因而無須考慮轉子損耗。但由于驅動方式的不同及齒槽效應的影響,轉子會產生損耗,并集中分布于磁極表層區域,從而導致該處熱源密度較大,引起轉子發熱,嚴重時會造成永磁材料去磁,影響電機的性能,縮短電機的使用壽命。
本文在上述分析研究的基礎上,計算了PMsM的鐵心損耗與磁極區域的渦流損耗,同時,也對兩類損耗對電機溫升的影響進行了分析。
1 PMSM定子鐵耗與磁極渦流損耗計算
1.1定子磁密波形有限元計算
應用時步有限元法對電機鐵心磁場進行數值計算,當電機旋轉360。電周期時,進行11個位置的磁場計算,即每隔36。電角度計算一次,可得到定子鐵心每一個剖分單元磁密的徑向分量B:和切向分量B在圖l定子鐵心上選取4、B、c、D、E五點,可得各點磁密波形變化規律,如圖2所示。
從圖2可以看出,除了齒中間點(B點)的磁場外,可以認為是純粹的交變磁場外,其它各點均為交變磁場和旋轉磁場共同作用而形成的磁場。因此,在電機鐵心損耗的計算中不僅要考慮交變磁場所產生的鐵耗而且要考慮旋轉磁場所產生的鐵耗。
1.2定子鐵耗計算
根據鐵耗分離理論,定子鐵心每個單元由任意磁密波形所引起的鐵心損耗包括磁滯損耗Phys、渦流損耗Pclass和附加損耗Pexe三部分,即:
Pcore=Phys+Pclass+Pexe (1)
借助于諧波分析原理,電機中任意點磁密波形都可分解成一系列的橢圓型諧波磁密矢量對于每一個k次諧波分量,長軸磁密為B kmaj,短軸磁密為B kmin,在計算由旋轉磁場產生的磁滯損耗時 [2],將旋轉磁滯損耗等效為兩個正交的交變磁滯損耗,因此,定子磁滯損耗的計算式: 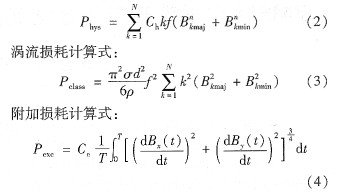 式中:Ch為磁滯損耗系數;n取2為計算磁滯損耗經驗系數;σ為鐵心迭片電導率;d為鐵心迭片厚;p為鐵心迭片密度;Ce為附加損耗系數。
根據時步有限元法計算得到的一個周期內每個單元磁密矢量B的波形,采用式(2)~式(4)可以得到該單元的單位質量鐵心損耗,再乘以該單元的質量就可得到此單元的鐵心損耗。總鐵心損耗等于各個剖分單元鐵心損耗之和。
1.3磁極渦流損耗計算
PMsM轉子磁極內的電磁場屬于低頻渦流場,對其進行分析時引入以下假設:(1)忽略位移電流的影響;(2)不計永磁磁極的自身磁化作用。基于上述假設,在整個求解區域中,二維正弦穩態電磁場可以用復數矢量磁位A所表達的渦流方程描述[4,5]:
定子鐵心外圓及轉子軛內圓邊界線上滿足一類邊界條件:A=O。式中:A為復矢量磁位;Js為源電流密度;v為磁阻率;σ為電導率;ω為轉差頻率。因此,根據電磁場
2 PMsM電機溫度場數值計算
2 1基本假設與邊值問題
求取電機運行時的穩態溫度場分布,考慮端部繞組的影響,以徑向任意齒的中心線為基準,取電機一個齒距的范圍,軸向半個鐵心段為求解區域,如圖3所示。
為簡化計算,作以下假設:(1)考慮定子繞組銅耗時,認為渦流效應對每根股線的影響相同,鐵心端面、槽絕緣端面及鐵心外表面的散熱系數分別取其平均值;(2)槽楔近似與槽同寬,槽內所有絕緣(股線絕緣、層間絕緣)性能均認為與主絕緣相同;(3)考慮端部繞組模型交叉影響,假設端部繞組熱源與槽內繞組熱源相等;(4)為方便端部模型建立,定子槽底圓弧部分用直線等效,槽內繞組為梯形分布。于是,穩態三維溫度場的邊值問題為:
式中:T為物體的溫度,℃;Kx、Ky、Kz為x、y、z方向的導熱系數,w/(mm·℃);q為熱源密度,W/mm3;Te為s面周圍介質的溫度,℃;α為s面的散熱系數,w/(mm2·℃)。
電機求解域的邊界條件為:(1)認為電機軸向中心段的中間斷面S1、齒中心斷面S2為絕熱面,應用絕熱邊界條件;(2)鐵心外表面與轉子軛內表面S3、S4、鐵心端面S5,、絕緣端面s6、涂層端面s7、磁極端面s8、轉子軛端面s9、定子端部繞組各表面s10。為散熱面,應用對流換熱邊界條件。
2.2損耗的確定
(1)額定電流時定子繞組的基本銅耗:
式中:Iφ和Ra75。分別為相電流和定子繞組每相電阻(75℃時)。
(2)額定電流時定子繞組的附加銅耗[8]:
式中:kr為并聯股線間的環流系數;m為相數;ks為渦流損耗系數;fN為頻率。
(3)鐵心損耗與轉子磁極表面損耗分別為前述磁場數值計算獲得值。
2.3散熱系數的確定
(1)軛背面:α=40 w/(m2·℃)
(2)定子鐵心及轉子各端面散熱系數為:
式中:Vn為強制風冷氣體介質的流速,自然冷卻時αn=22.22 w/(m2·0C)。
其它表面散熱系數可查閱相關文獻[8,9]計算得到,篇幅有限不再贅述。
3計算結果及分析
根據上述分析,本文應用二維和三維有限元法對某型PMSM的定子鐵耗、磁極渦流損耗及溫度場進行了計算。電機額定及結構數據如下:T=100 N。m;u。=272 V;nN=200 r/min;fn=53.333 Hz;D0=324 mm;D1=235 mm;L=32 mm;p=16;Z=99。定子繞組Y型連接,轉子采用無間隙表面貼片式磁極,自然冷卻。
3.1定子鐵耗計算結果
計及10次以下諧波分量,PMSM的鐵耗計算對比曲線及不同工況下的鐵耗值分別如圖4及表l所示,實驗數據由電機的空載實驗獲得。
圖4及表1中空載損耗包含了電機的機械損耗,因此實測值高于計算值。由對比分析可看出,本文采用的有限元法計算結果明顯高于經驗公式計算結果。另外,從表1還可以看出,當考慮旋轉磁場與諧波磁通影響時,磁滯損耗與渦流損耗比經驗公式計算下的相應損耗大幅提高。磁滯損耗增加了兩倍以上,說明在電機運行過程中旋損轉磁滯損耗占的比重較大,總的渦流損耗與附加損耗增加了近百分之50,總鐵耗增加了近一倍,更接近于實測值。顯然,在計算電機飽和鐵心損耗時,僅考慮交變磁場與基波磁通是不夠的。
3.2磁極渦流損耗計算結果
由于集膚效應的影響,為了準確計算渦流損耗,對磁極區域渦流場進行有限元分析時,要慎重考慮磁極的網格劃分,磁極外圓區域所剖分的網格尺寸應小于磁場的透人深度[4]。本文利用三角形單元對計算區域進行離散,剖分結果如圖5所示。
為了清楚地反映磁極內的渦流分布,這里只顯示磁極內各場量的分布情況。圖6分別為磁極內渦流和渦流損耗密度的分布圖。由圖中可看出,磁極
內的渦流和渦流損耗密度沿磁極的周向為不均勻分布,且沿著磁極徑向渦流和渦流損耗密度迅速減少,磁極內渦流和渦流損耗密度的分布比較復雜,這主要是由于進行渦流場分析時,不同磁極對應的定子齒槽位置不同以及集膚效應的存在,使得磁極內不同區域磁場分布不均勻造成的。已知渦流損耗密度,根據式(8)可計算得到額定工況下電機磁極渦流損耗為3.87 w,圖7為磁極渦流損耗占電機損耗比例分布圖(不計機械損耗)。
3.3溫度場計算結果
根據電磁場的計算所得到的各個部件的損耗以及已知每個部位的散熱系數,就可以對電機三維溫度場進行數值計算。
3.3.1定子鐵心損耗對溫度分布的影響
圖8、圖9分別為考慮與不考慮鐵耗影響時的電機定子溫度場分布圖。樣機在環境溫度150情況下額定運行,采用電阻法,實測穩定溫升為113℃。
由于樣機槽絕緣較薄,鐵心材料導熱良好,以及鐵心尺寸較小,雖然鐵心損耗在鐵心中是不均勻分布,但對電機定子總的溫度分布影響不大,
但會使電機總的溫升有所提高,因此在電機溫度場計算中要著重考慮鐵心損耗的影響。
3.3. 2磁極渦流損耗對溫度分布的影響
從圖10和圖11的對比中可以明顯地看到,忽略磁極區域渦流損耗,轉子磁極溫度會有明顯的下降,最多相差8℃左右。雖然渦流損耗值不大,但是損耗的集中分布,決定了磁極表層區域的熱源密度較高,對磁極溫升的影響較大,在實際設計時應盡可能計算準確。
4結論
(1)通過對電機定子磁場的數值計算可知,PMSM電機鐵心的磁密波形十分復雜,各段鐵心差異很大,鐵耗也不同。磁密脈動是鐵耗增加的主要原因,因此,為減少鐵耗必須盡量減少鐵心中磁密的脈動分量,這除了需要我們采取合理的電機結構設計外,更重要的在于選擇合理的驅動方式。
(2)為了準確計算電機鐵心損耗,對電機進行磁場分析是必要的。通過分析可知,電機鐵心中存在交變和旋轉兩種意義的磁場,由旋轉磁場產生的損耗占總的損耗比重較大,是不可忽略的,而且由于鐵心飽和,計算鐵損時必須考慮諧波磁場的作用。
(3)PMsM磁極內渦流和渦流損耗密度的分布比較復雜,這主要是由于定子齒槽位置不同以及肌膚效應的存在,使得磁極內不同區域磁場分布不均勻造成的。
(4)對于鐵心尺寸較小的電機,是否考慮定子鐵耗的不均勻分布,對電機定子溫度場的計算影響不大,雖然電機轉子總的熱源較小,但是磁極區域渦流損耗熱源的集中分布,對電機轉子溫度場的求解有較大的影響,在實際計算中此部分損耗要盡可能計算準確。
(5)通過電機溫度場的計算可知,自然冷卻的PMSM定、轉子溫度分布存在較大差異,定子的溫度明顯高于轉子,由于轉子溫度較低,對永磁體的性能不會有較大影響。
|