異步電動機矢量模型的Matlab軟件仿真及其應用
林琳,陳剛
(南京工程學院,江蘇南京211167)
摘要:利用Matlab simulink制作了異步電動機矢量控制仿真中所需的三個轉子磁鏈計算模型及異步電動機矢量模型,探討了這些模型的實際使用問題。為方便教學和學生實驗使用,還對這些模型進行了封裝。
關鍵詞:轉子磁鏈計算模型;異步電動機矢量模型;Mat1ab;Slmullnk
中圖分類號:TM343 文獻標識碼:A 文章編號:1004—7018(2008)0l一0031—04
O前言
目前對異步電動機控制系統進行仿真時,所用的異步電動機模塊取白Matlab slmulink庫中的異步電動機模塊,如圖l所示:異步電動機模塊,其拆封后的內部結構如圖2所示。從圖2人們看不出基于電機理論的異步電動機模塊內在結構。無論是對于研究還是對于教學來說,都是十分不便的。學生無法將教材上的異步電動機控制理論同所用模塊結合起來,而對于研究者,則無法選擇、調整模塊結構及參數值。
為此,利用Matlab simulink制作了異步電動機矢量控制仿真中所需的三個轉子磁鏈計算模型及異步電動機矢量模型,可供教學和做仿真時使用。在輸入定子電流及異步電動機參數的情況下,可以得到各物理量的輸出波形,將教材中抽象的微分方程轉變成直觀的物理量的輸出波形,會獲得更好的教學效果。這些模型還可以用來研究異步電動機的過渡過程,也可以用來構建各種控制系統。最后,為防止使用過程中對這些模塊進行誤修改,對這些模塊
進行了封裝,并添加了相應的說明,以方便實際使用。
1異步電動機矢量模型方程
按照異步電動機的實際物理模型所建立的動態數學模型是一個高階、非線性、強耦合的系統。直接分析和計算這樣的方程組是十分不便的,人們研究了不同的簡化分析方法,矢量變換法便是其中一種。矢量變換法的目的是模仿直流電機的控制機理,來對異步電動機進行控制:其基本思想是:首先進行坐標變換,包括三相靜止一二相靜止變換(3—2變換),即三相交流電流iA、iB、iC。變換成二相靜止坐標系上的交流電流iα、iβ;二相靜止二相旋轉變換(2—2變換),即二相靜止坐標系上的交流電流iα、iβ變換成二相旋轉坐標系上的交流電流id、iq,其中d軸沿著轉子磁鏈矢量的方向定向,q軸逆轉子轉向旋轉90。。具體坐標變換方程組如下。1.1三相靜止-二相靜止坐標變換方程二相靜上坐標系稱為α-β坐標系,取 軸與A軸重合,采用總功率不變的原則,則:
1.2二相靜止-二相旋轉坐標變換方程
二相旋轉坐標系取M-T坐標系,M軸與α軸的夾角即為φ角.
1.3二相旋轉坐標系下的磁鏈、電壓及電磁轉矩方程
1.3.1 磁鏈方程
二相靜止坐標系α-β上的磁鏈方程:
式中:Lms———三相坐標系中定、轉子每相繞組的****互感;
Lm————定、轉子同軸等效繞組間的互感, Lm=3/2Lm;
Lm————定子等效兩相繞組的自感,Ls=Lm+L1s;
Lm————定子等效兩相繞組的自感,Lr=Lm+L1r;
1.3.2電壓方程
二相靜止坐標系α-β上的電壓方程:
二相同步速旋轉坐標系M-T上的電壓方程:
式中:ω1——旋轉坐標系相對于定子側靜止坐標系A—B—c軸的電角速度;
ω——轉子旋轉的電角速度;
ω1-ω——旋轉坐標系相對于轉子側靜止坐
標系。a-b—c軸的電角速度。
1.3.3電磁轉矩方程
式中:P——極對數。
因為M軸沿轉子總磁鏈ψr的方向,T軸垂直于M軸,所以ψrm=ψr,ψrT=0。異步電動機由變頻器供電,設定子側三相電流iA、iB、iC為已知。由上述的二相旋轉坐標系下的磁鏈方程及電壓方程,消去irM,irT,ψsM,ψsT可得下述微分方程組:
2異步電動機仿真模型
異步電動機仿真的輸入量為變頻器輸出的對稱三相交流電流,輸出量為異步電動機的電角速度ω、電磁轉矩Te及轉子磁鏈ψr。
由式(8)可得: 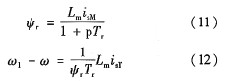 式(10)、式(11)是轉子磁鏈定向的異步電動機動態模型的微分方程。
從旋轉坐標變換開始,直至建立異步電動機仿真模型,我們必須掌握轉子磁鏈矢量的空問電角度φ及轉子磁鏈ψr的大小。由于種種原因,直接測量這些參數是不可能的,只有通過轉子磁鏈模型計算來獲得φ及ψr的數值。
2.1建立轉子磁鏈模型
利用定子側兩相坐標系上的電流或電壓及轉子角速度ω來計算φ及ψr.
2.1.1基于靜止坐標系的電流isα、isβ計算φ及ψr的電流模型
利用式(3)中兩個轉子磁鏈分量ψra、ψrB方程,以及式(5)中兩個轉子電壓分量ura,urb方程,消去其中的轉子電流ira,irb可得轉子磁鏈ψra、ψrB的計算公式:
依據式(13),可建立基于靜止坐標系上的計算轉子磁鏈的電流模型,輸入信號為電流isα,isβ輸出信號為φ及ψr。
2.1.2基于旋轉坐標系的電流isM、isT計算φ及ψr的電流模型
利用式(11)和式(12)可得轉子磁鏈ψr及φ的計算公式:
依據式(14),可建立基于旋轉坐標系的計算轉子磁鏈的電流模型,輸入信號為電流isM,isT輸出信號為Φ及Ψr。該模型要解決好除法環節初始狀態下除數為零的問題。
2.1.3基于靜止坐標系的電壓usα、usβ計算Φ及Ψr,的電壓模型
利用式(5)中靜止的兩相坐標系上的定子電壓usa、usb與電流的關系方程,以及式(3)中靜止的兩相坐標系上的兩個轉子磁鏈分量砂方程,消去其中的轉子電流及i。,可得基于電壓ψra、ψrB來計算的方程:圖13----依據式(15),可建立計算轉子磁鏈的電壓模型,輸出信號為Φ及Ψr。在硬件電路中,可以直接以定手電流和定子電壓作為輸入信號,而在仿真時,在僅有定子電流輸入的情況下,可以通過式(5)計算得到電壓usα,usβ,一起作為輸入信號。
以上三種轉子磁鏈計算模型從理論上講都是一樣的,但在實際應用中還是有差別的。電流模型、電壓模型應結合起來使用。
2.2異步電動機整體矢量仿真模型
三相定子電流iA、iB、iC作為異步電動機的輸入信號,電磁轉矩Te、轉子磁鏈Ψr,及轉速ω為輸出信號。依據式(9)~式(11),可得相應的異步電動機矢量仿真模型如圖3所示。設定異步電動機的參數為:R1=1.73Ω,X1σ=4 Ω,R2=1.04 Ω,X2σ=4Ω,Rm=4.46 Ω,Xm=61.1 Ω,IN=6.7 A。
構建異步電動機矢量仿真模型必須考慮如何利用三個轉子磁鏈計算模型。分別利用計算轉子磁鏈的靜態電流模型及動態電流模型構建異步電動機矢量仿真模型時,仿真均收斂,而單獨使用計算轉子磁鏈的電壓模型建立異步電動機矢量控制模型時,仿真不收斂。
這主要是由于電壓模型包含純積分環節,在低速時誤差較大。為此,采用電流模型與電壓模型相合的策略,即在低速時使用電流模型,高速時使用電壓模型。經過調試,獲得了收斂的異步電動機矢量控制模型。
3結語
分別利用三種異步電動機矢量模型,對異步電動機空載起動、負載運行進行仿真。從仿真結果來看,針對同一種運行情況,三種異步電動機矢量模型所得到的結果是一致的。限于篇幅,僅列出利用旋轉坐標電流模型與電壓模型結合的混合轉子磁鏈模型所得的仿真結果,如圖4所示。負載的加載時刻
通過波形圖可以看出,在t-3s時,時步電動機已基本進入穩定空載運行狀態,加上負載咒以后,電機經過一個過渡過程,進入穩定的負載運行狀態,Ψr有所降低,轉速也略有下降。可見,該仿真模型可以非常方便和直觀地研究異步電動機的過渡過程。另外,仿真模型也可以有選擇地被用來構建異步電動機的控制系統。
為便于應用模型,防止對模型無意的改動,有必要對模型進行封裝,并定制對話框和圖標。
|