遺傳優化的模糊免疫PID控制器在SRM中的應用
喬維德
(常州市廣播電視大學,江蘇常州213001)
摘要:針對開關磁阻電機驅動系統的嚴重非線性、時變和強耦合性.應用免疫反饋機理和模糊控制理論,在傳統PID控制器基礎上設計一種模糊免疫PID控制器,并提出利用遺傳算法對PID控制器參數進行優化設計方法。仿真結果表明,基于遺傳優化的模糊免疫PID控制器具有良好的調速和控制特性,其控制眭能明顯優于傳統PID控制和模糊免疫HD控制。
關鍵詞:開關磁阻電機;遺傳算法;模糊免疫PID;控制
中圖分類號:TM352 文獻標識碼:A 文章編號:1004—7018(2008)01—0008—03
0引言
開關磁阻電動機(簡稱SRM)調速系統是隨著電力電子技術、微電腦技術和控制技術發展起來的新一代交流無級調速系統,其顯著特點是電機結構簡單、調速范圍廣、起動轉矩大、調速和控制性能好、效率高。SRM在低壓和小功率的應用場合,大大優于普通的異步電動機和直流電動機,目前已引起了國內外學者的普遍關注和深入研究,并在很多領域得到了廣泛的應用。但SRM磁路的高度非線性決定了它是一個時變的、非線性系統,很難求得其精確的數學模型,所以應用傳統的線性控制方法(如PID控制)難以滿足動態較快的SRM非線性、變結構、變參數的要求。為了使SRM系統取得優良的調速性能和控制品質,本文將遺傳算法、模糊控制和免疫反饋機理與傳統的PID控制相結合,設計了一種模糊免疫自適應PID控制器,利用遺傳算法優化控制器參數,并將它應用于SRM調速系統中,借助MAT—LAB進行仿真實驗,其控制效果明顯優于傳統PID控制器和模糊免疫HD控制器,具有很強的魯棒性和自適應能力。
1 SRM基本原理
圖1是SRM的結構示意圖,定、轉子為雙凸極結構。如果將定、轉子的相對位置作為起始位置,依次讓定子B相繞組通電時,就會產生一個使鄰近轉子與該B相繞組軸線重合的電磁轉矩,轉子便逆著勵磁順序按逆時針方向連續旋轉;若依次給C相繞組通電,則轉子將順時針旋轉,因此,SRM的轉向取決于相繞組通電次序,而與相繞組的電流方向無關。
由于SRM是高度機電一體化的無級調速系統,包括電氣部分、機械部分和機電聯系部分,其數學模型描述為:
式中:Uk、Rk、ik、ψk分別為第k相繞組的電壓、電阻、電流和磁鏈。
(2)轉矩方程
式中:Wk、Tk分別為電機第k相的磁場儲能和產生的電磁轉矩;θ為轉子位置角;Ttotal為總的電磁轉矩(即各相轉矩之和)。
(3)機械運動方程
式中:J為系統轉動慣量,B為摩擦系數,TL為負載轉矩。
上述數學模型中,由于SRN存在嚴重的飽和效應、邊緣效應和非線性,加之運行時的開關性和受控性,無法建立比較精確的數學關系,因而傳統的線性控制方法已難以滿足SRM非線性、變參數的要求,不能取得理想的控制效果。
2 SRM驅動系統設計
SRM調速系統主要由SRM、功率變換器、控制器、位置檢測器等部分組成,控制器是系統的中樞,它接受速度指令、速度反饋信號及電流傳感器、位置傳感器等信息,并對其進行綜合分析處理,發出控制信號,實現對SRM運行狀態的有效控制。本文控制器采用遺傳算法優化的模糊免疫PID控制器。系統結構圖如圖2所示。
2.1免疫PID控制原理
免疫PID控制器是借鑒生物系統的免疫機理而設計的一種非線性控制器。根據免疫反饋機理,定義第A代的抗原數量為ε(k),由抗原刺激的來自增強T細胞TH輸出為TH(k):
式中:k1為激勵因子。假設Ts抑制細胞對B細胞的影響為Ts(k),則:
式中:k2為抑制因子;f(·)為非線性函數,反映抑制細胞Ts的抑制量。因此B細胞接收的總刺激為:
如果控制系統第k個采樣時刻給定值與輸出值的偏差e(k)和控制器的輸出u(k)分別對應于免疫系統第k代的抗原數量ε(k)和B細胞接收的總刺激s(k),則有如下的反饋控制規律,即:
式中:K為控制的響應速度,K=k 1,K越大,響應速度越快;η為控制響應的穩定性, 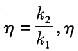 η增大,系統的超調量就減小;只要適當調整參數k和η,可使控制系統獲取較快的響應速度和較小的超調。 由此可見,基于免疫反饋機理的控制器實際上是一個非線性P控制器,該控制器是由一個基本的P型免疫反饋控制器和一個增量模塊組成,其比例系數Kp1隨著控制器輸出的變化而變化,具有很強的自適應能力。免疫PID控制器的輸出u(k)為:
微分系數。
2.2模糊免疫P1D控制器的設計
參數K、w和非線性函數f(·)的選取對控制器的性能有很大的影響。本文運用模糊控制器來逼近非線性函數fu(k),△u(k)),將免疫PID控制器的輸出u(k)和其變化量△u(k)作為該模糊控制器的輸入變量,輸出變量是Ts細胞的抑制量,f(u(k),△u(k))。
輸入變量u(k)、△u(k)與輸出變量f(u(k),△u(k))的論域取值均為7個語言值,即NB(負
大)、NM(負中)、NS(負小)、zE(零)、PS(正小)、PM(正中)、PB(正大)。考慮SRM轉速偏差范圍寬和高穩速精度的特點和要求,將偏差u(k)論域界定為19個等級,偏差變化量△u(k)和輸出控制量,f(u(k),△u(k))界定為11個等級,即:
根據sRM運行特性和操作經驗,建立模糊控制規則如表l所示。
模糊控制規則可以采用如下一組模糊條件語句來描述: If u is Ai △uisBjtherf,=cij(其中i=l,2...m;j=1,2,…,n)
設共有k條規則,因此得到:
這些模糊條件語句可歸納為一個總的模糊關系為:
根據模糊推理合成規則,輸出控制量的模糊集為Cij:(Ai×Bj).R。
3遺傳算法優化模糊免疫PID控制器
根據上面分析可知,基于免疫反饋機理設計的免疫控制器實際上就是一個非線性P控制器,由于存在著非線性干擾和噪聲等因素,在確定參數k1、η、ki、kd的取值時比較困難。目前參數優化方法很多,如文獻[1]提出的單純形法、專家整定法等,雖然這些方法都具有良好的尋優功能,但它們仍存在明顯的不足,如單純形法極容易陷入局部****解,專家整定法耗時長、速度慢,尋優效果差。而遺傳算法是一種基于自然選擇和群體遺傳機理的并行隨機搜索算法,它模擬了自然選擇和自然遺傳過程中的繁殖、雜交和變異現象,它并不需要任何信息,僅根據適應度函數值,通過遺傳進化就能得到全局****解。利用遺傳算法優化免疫控制器的步驟如下:
(1)參數編碼,確定每個參數的大致范圍和編碼長度。文中采用實數編碼,將免疫控制器的每一個參數k1、η、ki、kd作為個體中的一個基因,編碼長度等于其個體的個數。
(2)產生初始種群。基本遺傳算法的初始種群是隨機產生的,對解空間缺乏代表性。本文將各待優化參數取值范圍均勻分成群體總數個小區間,由每個初始個體在每個小區間中隨機選取出的具有代表性的值,隨機組合成新的基因串。新產生的各個個體均具有很強的代表性,而且還存在著明顯的差別,保證初始種群的多樣性,增大了搜索收斂于全局****點可能性。
(3)設計適應度函數。將個體實數編碼一一對應為免疫控制器的各個參數值,然后利用這些參數值并根據具體的控制要求,確定****指標函數J,適應度函數,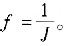
(4)采用選擇交叉和變異算子進行遺傳操作,產生下一代種群。基本遺傳算法中,采用固定的交叉概率和變異概率,搜索效率不高,且存在早熟現象。本文設計了自適應變化的交叉概率Pc、變異概率Pm。交叉概率Pc和變異概率Pm能基于個體適應度自適應地進行調整,保證了遺傳算法的收斂能力,并使其收斂速度加快。自適應交叉概率Pc和變異概率Pm計算公式為:
式中:fmax為每一代群體中****適應度函數值;f為每代群體的平均適應度函數值;f為要交叉的兩個交叉個體中較大的適應度函數值;f為要變異個體的適應度函數值;K1、K2、K4心為常數(≤1)。
(5)結束條件判斷。若滿足結束中止條件,則結束遺傳進化過程,否則返回第(4)步。
4仿真實驗研究
為了進一步說明和驗證遺傳算法優化的模糊免疫控制器在SRM驅動系統中的應用情況,在不同工作條件下,利用MATLAB語言進行計算機仿真分析。SRM仿真參數為:三相6/4極,額定相電流為I=5 A,額定轉速為n=l 500 r/min,定子電阻為R=3.4Ω,額定轉動慣量為J=0.000 16 kg·m2。模糊免疫PID控制器的參數值根據經驗設定為:K=O.27,η=O.08,ki=O.5,kd=0.2。為方便比較起見,傳統PID控制器參數與模糊免疫PID控制器參數應選取一致,由Kp1=K[1-ηf(u(k),△u(k))]和傳統PID的f(·)=0,得Kp1=K=0.27,所以傳統PID控制器參數選定為:kp=0.27,ki=O.5,kd=0.2。遺傳參數為:初始種群規模為50,交叉概率Pc=O.86,變異概率Pm=O.02,進化迭代次數為100。經過遺傳算法優化后得到的模糊免疫PID控制器參數的****值為k=0.506 3,η=O.062 5,Ki=1.854 2,Kd=O.014 7。圖3中的傳統PID
控制、模糊免疫PID控制和遺傳優化模糊免疫PID控制三種情況下的速度階躍響應曲線(給定轉速l 500 r/min并在t=l. 0 s時加一擾動量),從仿真結果可以看出,采用遺傳算法進行模糊免疫PID控制器參數尋優設計時,得到的控制系統的穩定性好,響應速度快,調節時間短,超調量小,魯棒性和抗干擾能力強,其控制效果明顯優于傳統PID控制和模糊免疫PID控制。
|