無軸承同步電機通用旋轉磁懸浮力模型研究
卜文紹1,2,黃聲華1,萬山明1,吳芳1
(1.華中科技大學,湖北武漢430074;2.河南科技大學,河南洛陽471003)
摘要:解析了無軸承電機的通用電感模型,導出了通用同步速旋轉磁懸浮力模型。該通用模型可同時適用于凸極型轉子和圓柱型轉子無軸承同步電機,仿真驗證了模型的正確性和有效性。
關鍵詞:無軸承同步電機;旋轉磁懸浮力;通用模型
中圖分類號:TM341 文獻標識碼:A 文章編號:1004—7018(2008)01—0001—03
0引言
無軸承電機是適合于高速運轉場合的新型電機[1-6]。在高速運轉中,難免會因轉子質量偏心產生不同程度的周期性離心振動。所以克服周期性離心振動是無軸承電機在高速領域廣泛應用的關鍵問題之一。各類無軸承電機都具有相同或近似的磁懸浮特性和規律,柱形轉子可看作凸極轉子的一種特例。本文將以具有勁弧寬的凸極型轉子無軸承同步機作為一般化結構模型,詳細推導出二極浮控四極無軸承電機的電感模型和通用同步速旋轉磁懸浮力模型。
1無軸承電機通用電感模型
1.1解析氣隙磁通分布規律
若在靜止坐標系下的轉子中心坐標為(α,β),則沿轉子外表面的單位弧度氣隙磁導為[2]:
式中:θ為沿定子內表面逆時針機械角度;δ0為單邊平均氣隙長度;l為轉子長;R為轉子外半徑。
式(1)僅適用于轉子凸極覆蓋的氣隙區域。圖1中的轉子凸極覆蓋氣隙區域可表示為:
其中:φ為轉子實際旋轉的機械角度;p為轉子凸極弧寬的一半。圖1還給出了一般化無軸承同步模型
電機的各繞組(軸線)位置分布及電流參考方向。圖中,四極電機a相繞組和二極浮控α相繞組的軸線重合于α坐標軸的軸線位置處,則沿氣隙圓周各等效正弦繞組的匝數分布規律為:
其中:N4q和N2q分別為四極(等效)正弦電機繞組和二極(等效)正弦浮控繞組的每極每相串匝數。
若忽略磁飽和及磁路壓降,根據高斯定律,可計算出各轉子磁位表達式:
則在Ω氣隙范圍內,由各繞組電流產生的氣隙磁通分布解析規律為:
1.2靜止坐標系下的電感矩陣解析模型
根據磁鏈和繞組電流的關系,可定義出四極轉矩繞組自感矩陣L4s、二極浮控繞組自感矩陣L2s和兩套繞組問的耦合互感矩陣M42s:
根據式(1)~式(3),可計算得到靜止坐標系下的二極浮控四極無軸承電機各電感矩陣模型為:
其中:矩陣L2s中,約等式成立的條件是轉子偏心率的平方遠小于O.5,該條件在無軸承電機懸浮運轉中一般都能滿足。
式(5)中,各電感系數通用解析算式為:
式中:α和β為轉子沿靜止坐標軸向的偏心位移。
1.3轉子坐標系下的電感矩陣解析模型
坐標系定義:xy坐標系為機械空間內的以同步速旋轉的坐標系,原點設在定子中心線上。
采用如下旋轉坐標變換:
可得到同步旋轉坐標系下的通用電感矩陣模型:
式中:矩陣L2r中,約等式成立的條件同式(5)。x、y為轉子軸心沿xy同步旋轉坐標系各軸向的徑向偏移量;各電感系數算式參考式(6)。
從式(7)可知:①在xy旋轉坐標系下,無軸承電機各電感矩陣解析模型中不再含有時變量φ,因而便于實際應用;②在不考慮磁飽和的情況下,在電機繞組和懸浮控制繞組的互感矩陣中,各個互感元素是轉子徑向位移量的線性函數。
2同步速旋轉磁懸浮力通用控制模型
坐標系定義:①dq坐標系為四極電機磁場同步旋轉坐標系;②jk坐標系為二極懸浮磁場同步旋轉坐標系;③兩套坐標系共同對應于機械空間內同一個坷同步速旋轉機械坐標系。
設:i4d、i4q為無軸承同步電機四極轉矩系統合成電流矢量的d、g軸分量;i2j、i2k。為浮控繞組在廬坐標系下的懸浮控制電流分量。取電流向量:z=[i4d,i4q,i2j,i2k]T,在忽略電機磁飽和的情況下,電機氣隙磁場儲能可表示為:
根據虛位移原理,作用于轉子上的徑向電磁力為:
根據式(7)~式(9)可導出沿巧各坐標軸向的同步速旋轉磁懸浮力通用控制模型為:
式中:M和M1的通用模型解析算式參考式(6)。
該磁懸浮力模型為沿砂同步速旋轉機械坐標系兩坐標軸向的磁懸浮力解算模型,可用于無軸承同步電機的周期性離心振動控制。
3通用模型的應用及仿真驗證分析
3.1圓柱型轉子無軸承電機旋轉磁懸浮力模型
四極圓柱型轉子結構相當于 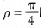 時的凸極型轉子結構。將圖 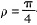 代人式(6),得電感系數: 將式(11)代人式(10),可得同步速旋轉磁懸浮力模型:
3.2凸極型轉子無軸承電機旋轉磁懸浮力模型
以極弧寬度為 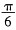 的無軸承同步磁阻電機為例。首先將極弧寬度參數 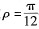 代人式(6),得到相應的電感系數計算模型: 將式(13)代人式(10),可得同步速旋轉磁懸浮力模型:
式(12)和式(14)中:i4d、i4q分別為dq坐標系下四極轉矩系統的d軸激磁電流和q軸轉矩電流;i2j、i2k為jk坐標系下的二極浮控電流。
3.3旋轉磁懸浮力模型有限元仿真驗證分析
鑒于篇幅,本節僅應用電磁場分析軟件針對凸極同步磁阻型無軸承電機進行仿真驗證和分析。
電機主要參數:定子24槽,氣隙O.6 mm;轉矩繞組:p 1=2,雙迭,單圈匝數24,額定電流5 A;浮控繞組:p 2=1,單迭,單圈匝數16;凸極參數 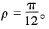 按式(14)和仿真值繪出的沿x軸向懸浮力曲線對比如圖2所示。沿其他方向的曲線對比也可類似繪出。 從曲線可知:在一定控制電流范圍內,仿真計算結果與模型計算結果差別不大;控制電流2 A時,誤差大約百分之6;當控制電流進一步增加時,開始出現明顯非線性偏移。這是由于凸極轉子的導磁區域相對較窄,易達到磁飽和的原因。但在非磁飽和區域,兩條吐線的較好趨近性仍可證明式(14)的合理性和正確性。
4結語
本文以凸極弧寬為2p弧度的凸極轉子結構無軸承同步電機為一般化結構模型,推導出了二極浮控四極無軸承同步機的通用電感模型和通用同步速旋轉磁懸浮力線性解析模型。該通用模型既適用于凸極型轉子結構無軸承同步電機,又適用于圓柱型轉子結構無軸承同步電機。本文還針對凸極同步磁阻型無軸承電機進行了仿真驗證和分析,驗證了通用模型的正確性和合理性。為進一步深入研究無軸承電機的共性規律、基礎理論、動態運行特性分析及無軸承電機周期性慣性振動控制打下了一定理論基礎。
|