少妇被躁爽到高潮-亚洲熟女少妇一区二区-少妇无码太爽了在线播放-1000部禁片未18勿进免费观看

基于模糊PID的交流電動機矢量控制系統

曹海波，方建安，劉洪瑋

  (東華大學，上海201620)

    摘要：交流電動機矢量控制系統是一個非線性、強耦合、時變的復雜系統，用傳統的PID難以達到理想的控制效果：基于模糊控制原理與傳統PID原理相結合設計了模糊PID控制器。仿真結果表明，采用模糊PID控制器比采用常規PID控制器具有更好的動穩態性能。

    關鍵詞：矢量控制；模糊控制；PID控制；模糊PID控制；交流電動機

    中圖分類號：TM34  文獻標識碼：A  文章編號：1004—7018(2010)01—0064—03

0引言

    交流電動機結構簡單、成本低，安裝環境要求低，適于易燃、易爆、多塵的場合，尤其是在大容量、高轉速應用領域，備受青睞。但是交流電動機是一個多輸入多輸出(MIMO)、非線性、強耦合且時變的被控對象，由于被控對象的復雜性，直接導致了交流電機轉矩控制的困難。通過矢量控制，將交流電動機等效成直流電動機，從而獲得較好的轉矩特性。

近年來，眾多學者對如何使電機矢量控制的效果更加顯著進行了相關的研究，如在矢量控制的基礎上采用模糊控制器^[1]。模糊控制是一種基于規則的控制，在設計中被控對象不需要建立精確的數學模型。模糊控制器可以獲得良好的動態特性，但無法消除系統的靜態誤差。

  本文在分析矢量控制的基礎上，結合常規PID控制器和模糊控制器的特點，采用模糊PID控制器，建立相應的電機調速模型。通過與傳統的PID矢量控制模型進行比較，詳細說明該模型的特點。

1交流電動機矢量控制

    以產生同一的旋轉磁動勢為準則，交流異步電動機的定子交流電流i_a、i_b、i_c，通過三相／--相變換可以等效成兩相靜止坐標系上的交流電流i_α和i_β，再通過同步旋轉變換，可以等效成同步旋轉坐標系上的直流電流i_d、i_q：

    按照轉子磁鏈定向條件時交流電動機模型，取d軸沿著轉子磁鏈矢量ψ_r方向，為M軸；T軸為逆時針轉90。，垂直于矢量ψ_r。由于是以轉子磁鏈ψ_r方向作為M軸的方向，此時有ψ_rd=ψ_rM=|ψ_r|,ψ_rq=ψ_rT=0。得到此時電磁轉矩和電壓方程為：

式中：p為極對數；L_m為互感；L_r為轉子電感；L_s為定子電感；R_s為定子電阻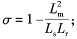；；p為微分算子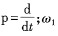， 為同步角轉速；ω_r為電機轉子轉速；ω_s。為轉差角轉速；。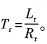

     由以上公式可以得到以下結果：

    轉子磁鏈ψ_r僅由定子電流勵磁分量i_sM產生，與轉矩分量i_sT無關。式(5)還表明ψ_rm與i_sM之間的傳遞函數是一階慣性環節。當勵磁電流分量i_sM突變時，ψ_r的變化要受到勵磁慣性的阻撓，這和直流電機勵磁繞組的慣性作用是一致的。

    轉子磁鏈的位置可由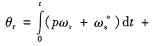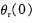

    得出，對于交流異步電動機，由于其轉子磁鏈的初始位置θ_r(0)是由定子電流決定的，如果系統運行時就采用矢量控制，則可以認為θ_r(0)=O。得到磁鏈位置θ_r后，可以通過旋轉變換得到勵磁電流分量i_sM，進而根據式(5)求得砂ψ_rM，并實施反饋控制^[2]。

    圖1是根據上述原理建立的系統仿真圖。異步電動機由電流控制PWM逆變器供電驅動，轉速控制器根據給定轉速與實測轉速之差，得到轉矩期望值T_e；轉矩電流分量i_sT由轉速控制器的輸出T_e和轉子磁鏈估計值ψ_rM進行計算；i_sT和i_sM經過逆旋轉變換和2／3變換，得到三相電流給定值i_a、i_b、i_c。i_a、i_b、i_c與實測三相電流i_a、i_b、i_c作為電流控制器的輸入，電流控制器輸出逆變器PWM觸發信號，控制逆變器驅動異步電動機運行。

2模糊PID控制

    傳統的PID控制算法結構簡單，對于大多數的控制過程都具有良好的控制效果和魯棒性，參數物理意義明確，理論分析體系完整且應用經驗豐富，因此被廣泛應用于實際工程當中。但是，常規PID控制器對于非線性、時變的系統和模型不清楚的系統無法進行很好的控制，其PID參數不是整定困難就是根本無法整定，而無法得到預期的控制效果。

    模糊控制是一種基于規則的控制，直接采用語言型控制規則，在設計中不需要建立被控對象的精確的數學模型，因而使得控制機理和策略易于接受與理解，設計簡單，便于應用。由工業過程的定性認識出發，比較容易建立語言控制規則，因而模糊控制對那些數學模型難以獲取、動態特性不易掌握或變化非常顯著的對象非常適用。

    但是模糊控制也有其自身不可克服的缺點，模糊控制器的輸出一般與誤差及誤差變化量有關，因此這種控制器只有比例一微分作用，沒有積分環節，理論上很難克服穩態誤差。如果把兩者結合起來，就可以構成兼有兩者優點的模糊PID(Fuzzy—PID)控制器。所以，針對被控對象的特性，我們選擇利用模糊控制器來給PID控制器在線自整定PID參數，組成模糊自整定參數PID控制器的控制策略。

    模糊PID控制主要是找出在不同時刻時PID的三個參數與e和e_c之間的模糊關系，在運行中不斷檢測e和e_c，根據模糊控制原理來對三個參數進行在線修改，以滿足不同e和e_c對控制參數的不同要求，從而使得被控對象具有良好的動、靜態性能。

    PID參數的整定必須考慮到不同時刻三個參數的作用以及相互之間的關系。由傳統經驗可知，在控制過程對參數k_p、k_i、k_d的自整定要求如下：

    當偏差|e|較大時，為了加速系統的響應速度，應取較大的k_p；同時為了避免由于開始時偏差e的瞬間變大可能出現的微分過飽和而使控制作用超出許可范圍，應取較小的k_d；同時為了防止系統響應出現較大的超調，應對積分作用加以限制，通常取k_i，=0，去掉積分作用。

    當|e|和|e_c|處于中等大小時，為了使系統響應具有較小的超調，k_p應取小一點，k_i、k_d的取值要大小適中，以保證系統的響應速度。

    當|e|較小即接近設定值后時，為使系統具有良好的穩態性能，應增加k_p和k_i的取值，同時為避免系統在設定值附近出現振蕩，并考慮系統的抗干擾性能，當|e_c|較小時，k_d取值應較大些，當|e_c|較大時，k_d取值應較小些。

    偏差變換率|e_c|的大小表明偏差的變化率，|e_c|值較大，k_p取值越小，k_i取值越大^[3]。

    針對矢量控制的轉速控制，在模糊規則中，誤差e、誤差變化e_c和修正系數k_p、k_i、k_d語言變量值取{NB，NM，NS，ZO，PS，PM，PB}，e和ec的論域均為(一6，6)，kp、k_d的論域均為(-1，1)，k_i的論域為(-O．5，O．5)，隸屬度函數呈三角分布。

    為了獲得精確的控制量，要求模糊方法能夠很好地表達輸出隸屬度函數的計算結果。本文采用工業控制中廣泛使用去模糊方法之一的加權平均方法。該方法針對論域中每個元素xi,以它作為待判決輸出模糊集合的隸屬度u(i)的加權系數，即取乘積xiu(i)，再計算該乘積和∑_xiu(i)對于隸屬度和的平均值x_o，即: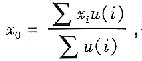，平均值x₀便是應用加權平均法為模糊集合求得的判決結果。最后用輸出量化因子乘以x₀，從而得到控制量的實際值。

    輸入到PID控制器的實際參數則為：

3仿真結果及分析

  設定異步電動機參數為：額定功率P_n=500 w；額定相電壓V_n=127 V；極對數P=2；定子電阻R_s=4．495 Ω；轉子電阻R_r=5.365Ω；定子電感L_s=0．165 H；轉子電感L_r=O．162 H；互感L_m=0.149 H；轉子慣量，J=O．00 095 kg·m²；粘滯阻力系數B=O。電流控制器滯環寬度為h=O．2 A；直流母線電壓為V_dc=350 V；系統中積分器與傳遞函數離散化采樣周

期為T_s=2μs[4]。設定轉速控制器k_p=10，k_i=26，k_d=10。

    通過Matlab／Simulink對電機矢量控制進行建模，對異步電動機進行空載變速及恒速加載運行仿真[5]。

    圖3和圖4為電機空載條件下運行時的仿真曲線，圖5和圖6為在0．3 s時給電機忽加T₁=8 N·m負載時的仿真曲線。從圖3中可以清楚地看到，當轉速控制器為普通PID時，電機轉速在O．3 s時達到穩定輸出狀態，電機轉矩在O．06 s時保持為零。當轉速控制器為模糊PID時，從圖4中可看到，電機轉速在0．25 s時即達到穩定輸出狀態，電機轉

矩O．04 s時即保持為零。

    從圖5中可以看出，普通HD加人負載時，電機轉速存在一個明顯的瞬時跌落過程，轉速在O 8 s中達到穩定，電機轉矩約在O．5 s時輸出保持穩定。 

     仿真結果表明，模糊P1D的動態響應快，穩態跟蹤精度高，轉矩具有瞬時響應特性。當電機功率越大，所帶的負載越大，其效果將更加明顯。

4結語

    將傳統的PID控制器與先進模糊控制相結合，既保持了傳統PID控制器結構簡單的優點，又把模糊控制有效地應用到了PID參數調節中，實現了系統的****控制。仿真結果證明了采用模糊PID控制，系統的響應速度加快，調節精度提高，穩態性能變好，而且沒有超調和振蕩，具有較強的魯棒性，這是普通PID控制難以實現的。它在非線性、時變的而圖6中，模糊PJD加入負載時，電機基本上保持原來轉速，瞬時跌落不明顯，電機轉矩約在0．4 s時輸出保持穩定。