式中:E一材料彈性模量(GPa):G 材料切變模量(GPa);p一材料密度(kg/m3);I 梁對中心軸的慣性矩(m4);A一彎曲梁的截面積(m。):k, 與梁截面形狀有關的常數,矩形截
面時k—O.833,圓形截面時k,=0.901。自由一自由梁的彎曲振動方程:
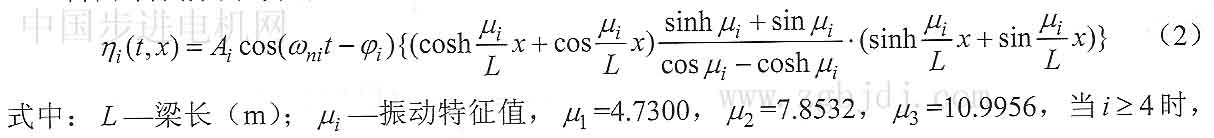
A1與振動幅值有關的系數W一彎曲振動共振角頻率(rad/s);竹一激振信號與振動啊應間相位差(rad)。
將(2)微分后代入(1)式得:

同理可表述為,式中各參數含義同前所述。
由式(6)分析得,當梁的徑長比較小,即為細長梁時,修正系數日,趨近于1,無需修正;當梁的徑長比較大時,修正系數O<Ⅳ,<1,需要考慮轉動慣量與剪切變形對固有頻率的影響,應
當對不考慮轉動慣量與剪切變形時的固有頻率進行修正。
1 2不同解析公式的比較
(I)(II)(III)分別為已發表論文和本文用于自由.自由彎曲振動梁共振頻率計算的解析公式。

上述三種解析公式形式相同,都可表示為不考慮轉動慣量與剪切變形時的固有頻率∥與相應修正系數H,的乘積。但文蒯[91k5文獻[10]在求解過程中,用到了細長梁的假設條件,使得(I)、(II)式只能適用于一定徑長比下的自由一自由彎振梁的同有頻率求解。具體為:將(III)在O處利用麥克勞林公式展開,取展式前兩項可得(I)、(II)。由數學知識可知,要使展開式保持高
的計算精度,應滿足掣(1+—生)趨近于o,即掣(1+—生)。設粱9 45號鋼等截面實心圓.
關于三種解析公式的進一步比較見表1與圖1。以45號鋼圓形截面梁為例,解析公式中相關參數取值情況見表l。
表1公式中參數取值情況
由表l參數及(I)、(II)、(III)式繪制一階彎振修正系數H1與徑長比D/L的關系曲線,見圖1。由圖1可知,當D/L d一0.3時,三種解析公式的修正系數值相差不大,進一步體現為
固有頻率計算結果一致性較好,表明此時三種解析公式都可以用于自由一自由超聲定子彎髓振動共振頻率的計算;當D/L分別大于O 65 Ej 0.8時文獻[1。10l Jl與文刮t219]中的解析公式修正系數值為負,與實際不符。
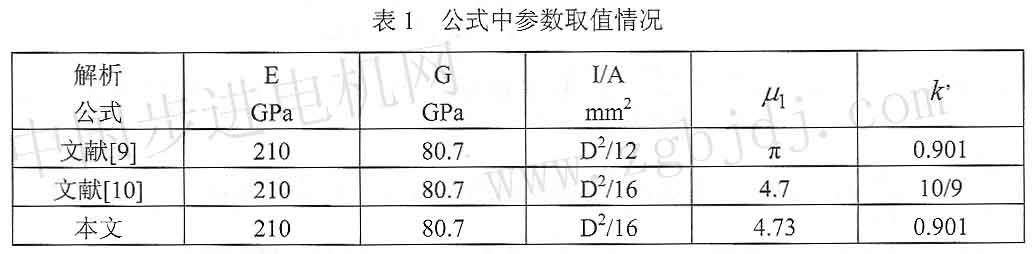
圖2為45號鋼、實心圓截面梁的r、二、三階彎睦振動F,本文解析公式中修正系數“z與徑長比關系曲線。
由圖2可知.對于任意D/It,修正系數均為正值,表明本文推導的解析公式在理論上可以用于任意D幾值下的彎曲振動梁的共振頻率的計算。對于相同振動階次,隨徑長比D/I。的增大,轉動慣量與剪切變形對共振頻率的影響越顯著,表現為修正系數值越小;對于相同的徑長比振動階次越高,轉動慣量與剪切變形對共振頻率的影響越顯著,亦表現為修正系數值越小。
2有限元仿真
ANsYs作為目前通用的仿真軟件,普遍認為其仿真結果是比較可靠的。為驗證解析公式,首先通過ANsYs仿真進行驗證。對于彎曲旋轉超聲波電動機,通常利用定子的一階彎曲振動模
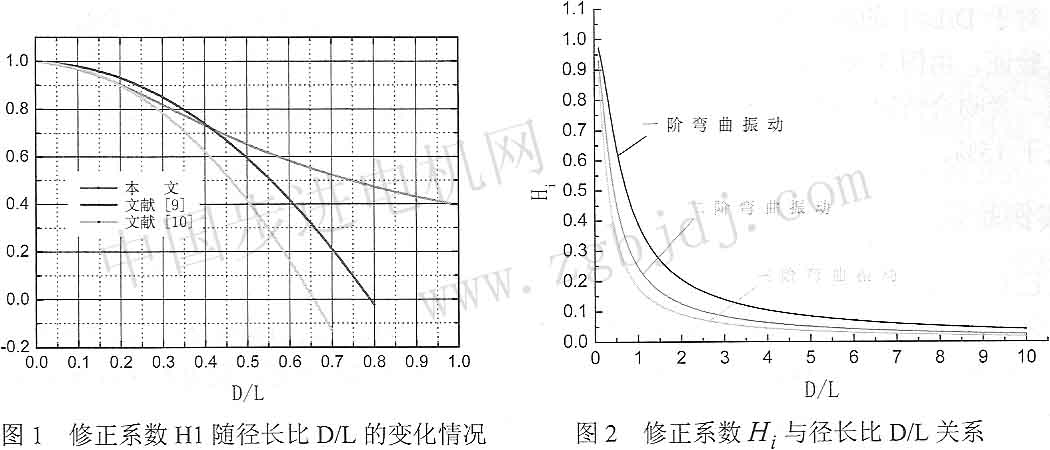
態實現電機驅圖3 a),b),c)分別是眭度為25mm、50rm、100mm,內外徑比為0 5的圓形截面梁,采用解析公式及利用ANsYs仿真,所得一階彎曲振動頻率與徑長比D/L關系曲線,其中所用材料均為45號鋼。
圖3解析公式與ANsYs仿真結果對比
對于D/L>l的梁,在實際中其彎曲振動模態較少利用,故只對徑長比O率值二者吻合情況較理想。當O 63實例驗證
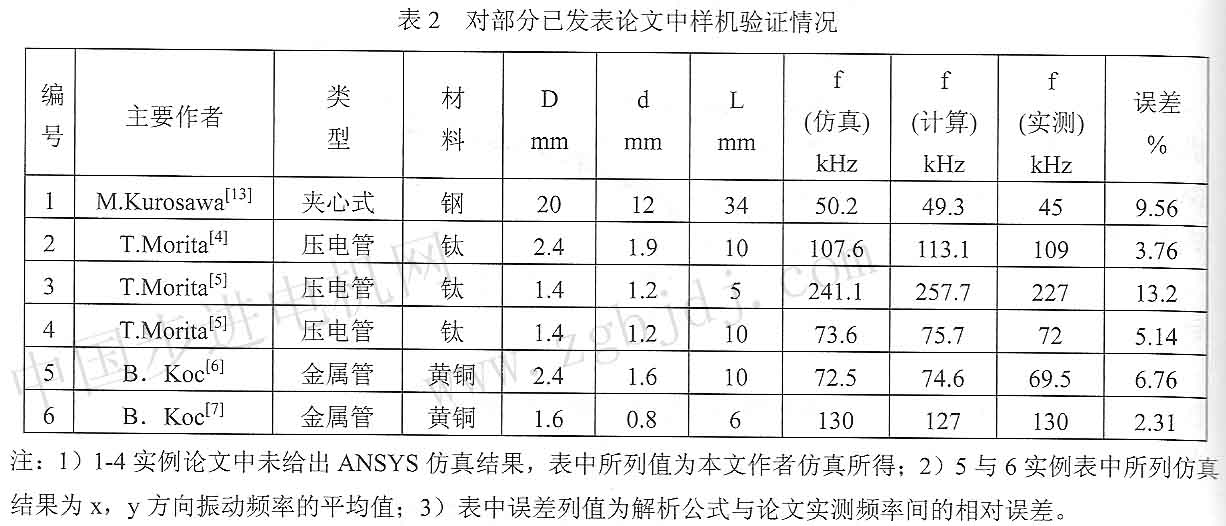
3 1已有樣機驗證
表2為對部分已有彎曲旋轉超聲波電動機樣機采用解析公式的驗證情況。由表2可得,ANsYs仿真、解析公式計算及樣機實測三者所得共振頻率值吻合’隋況較好,說明本文推導的解析公式兵有指導彎曲旋轉超聲波電動機定子設計的實際意義。
3 2實驗驗汪
圖4為作者母瞞0出的一臺金屬管式超聲波電動機定子”。定子外徑42mm,內徑34mm,長44mm,由金屬管與壓電陶瓷片粘貼而成,其中金屬管為鋁基體,壓電陶瓷為Pz4,定子徑長比D/L=095。
考慮定子是由硬鋁與Pz4構成的復合梁,通過計算兩種材料所占的體積比,建立定子的復合梁等效模型。利用解析公式計算其一階彎振頻率約為36 2kHz,ANsYs仿真結果為35 5kHz,實測工作頻率為30 0kHz。

圖4金屬管定子
前文的仿真結果均大于計算結果,而此處計算結果火于仿真結果。作者認為產生誤差的原因,主要來源于建立金屬基體與壓電材料的復合梁模垂的建立方法以及精確程度。關于復合梁等效模型的精確建立這一問題,正在進一步研究中。需要說明的是,若利用文獻[9]與文獻[10]中解析公式對該定子的共振頻率進行計算,所得計算結果為負值。
4結論
彎曲旋轉超聲波電動機定子,當其外徑與長度的比值增大時,轉動慣量與剪切變形對彎曲振-動共振頻率的影響將不能忽略。本文在對自由一自由鐵摩辛柯梁彎曲振動理論分析的基礎上,推導出考慮轉動慣量q剪切變形時、用于較大徑長比范圍內的共振頻率計算的解析公式。通過ANSYS仿真及實例驗證,結果表明仿真、驗證及解析計算j者所得一階彎曲振動頻率值吻合情
況較好,證明了解析公式的正確性,為彎曲旋轉超聲波電動機定子的設計與振動特性研究提供了理論依據。
