| 新型雙定子直線振蕩電機特性分析
于明湖,葉云岳,夏永明,張玉秋
(1浙江大學(xué),浙江杭州310027; 2.浙江理工大學(xué),浙江杭州310000)
摘要:新型雙定子動磁式直線振蕩電機具有結(jié)構(gòu)簡單、效率高,鐵心疊裝方式簡單等優(yōu)點。文章介紹了所研制的此新型雙定子直線振蕩電機的本體結(jié)構(gòu),并在此基礎(chǔ)上對其進(jìn)行了數(shù)學(xué)建模。對于其磁路模型,動力學(xué)模型以及驅(qū)動電路模型進(jìn)行了求解,揭示了電機及驅(qū)動系統(tǒng)各個參數(shù)對于電機性能的影響,為下一步的電機優(yōu)化設(shè)計以及控制系統(tǒng)設(shè)計奠定了基礎(chǔ)。
關(guān)鍵詞:雙定子;直線振蕩電機;優(yōu)化設(shè)計;數(shù)學(xué)建模
1介紹
在實際應(yīng)用中,我們常常需要些高頻往復(fù)運動的驅(qū)動機構(gòu)。以往這種驅(qū)動機構(gòu)往往是通過旋轉(zhuǎn)電機加曲柄連軸等中間轉(zhuǎn)換機構(gòu)獲得的。這種方式由于中間轉(zhuǎn)換機構(gòu)的存在加大了傳動損耗使得效率較低,并且噪聲大,壽命短。而直線振蕩電機可直接產(chǎn)生高頻往復(fù)運動[1],無需中間轉(zhuǎn)換機構(gòu),簡化了機械結(jié)構(gòu),效率較高。因此,直線振蕩電機特別是最近幾十年隨著永磁材料發(fā)展起來的永磁直線振蕩電機成為發(fā)展趨勢。而對于直線振蕩電機的結(jié)構(gòu)而言,由于動圈式以及動鐵式結(jié)構(gòu)均存在難以克服的缺點,因此日前研究熱點在于動磁式結(jié)構(gòu)。但目前已提出的許多結(jié)構(gòu)均存在各種問題,例如效率不高,裝配難度大等缺點。本文針對已存在電機結(jié)構(gòu)的問題,在吸取已存在電機結(jié)構(gòu)優(yōu)點的基礎(chǔ)上介紹了一種新型雙定子直線振蕩電機結(jié)構(gòu),此電機采用了反向磁通電機的運行原理。具有普通旋轉(zhuǎn)電機的定子結(jié)構(gòu),鐵心疊裝簡單,裝配難度小,降低了加工成本目.具有已投入實用的LG電機的高效率等優(yōu)點
本文首先針對電機結(jié)構(gòu)的特點,建立了其機電系統(tǒng)模型,通過對其以及后面機電系統(tǒng)模型的分析揭示了電機及驅(qū)動系統(tǒng)參數(shù)對于電機性能以及運動特性的影啊。由于彈簧的使用,此雙定子直線振蕩電機構(gòu)成了一個受迫振動系統(tǒng)。而眾所周知,電機供電電路本身也構(gòu)成了一個類似的二階系統(tǒng),從控制原理來講,兩者的傳遞函數(shù)是相同的,因此可將機電兩套系統(tǒng)進(jìn)行類比分析。本文將機械與電路系統(tǒng)兩個二階函數(shù)進(jìn)行了綜合分析并進(jìn)行了理論推導(dǎo)。此分析結(jié)果為對進(jìn)一步的此電機無位置傳感器控制算法設(shè)計以及電機的進(jìn)一步優(yōu)化設(shè)計奠定了基礎(chǔ)。
2雙定子直線振蕩電機本體結(jié)構(gòu)及磁路建模
2 1雙定子直線振蕩電機本體結(jié)構(gòu)
如圖1所示,電機包含兩個旋轉(zhuǎn)電機定子鐵心,定子鐵心之間相隔一段距離,沿軸向同心排列。定子由機殼、定子擋板及電機端板固定。電機端板上裝有直線軸承,動子通過直線軸在直線軸承的支撐下左右移動。動子兩側(cè)裝有共振彈簧。
如圖2所示,動子鐵心由硅鋼片疊裝而成,表面沿圓周等間隔安裝6塊永磁體,每個永磁體
的外圓周面與電機定子齒一一相對,定子采用用集中式繞組。從端面來看,此電機結(jié)構(gòu)類同于集中繞組式永磁旋轉(zhuǎn)電機。當(dāng)一端通入交變電流后,由于磁阻力的作用易產(chǎn)生旋轉(zhuǎn)運動。而采用了繞組繞向相反的兩個定子后,產(chǎn)生的旋轉(zhuǎn)力方向相反,旋轉(zhuǎn)力相互抵消。雙定子直線振蕩電機采用了繞組繞向相反的兩個定子,當(dāng)繞組通入電流后,兩定子對應(yīng)的磁極極性均相反,因此必然對于動子一側(cè)產(chǎn)生增磁,一側(cè)產(chǎn)生弱磁效應(yīng)。從而使得動子往增磁一側(cè)運動,當(dāng)通入交變電流后,動子跟隨電流同頻運動,因此此電機屬于永磁同步電機范疇。而由于雙定子繞組繞向相反,總電感在動子運動過程中不變,因此,動子是在電磁力作用下往復(fù)運動。
2 2雙定予直線振蕩電機電磁推力解析推導(dǎo)
由磁共能理論,電機電磁推力等于繞組電流保持恒定情況下,磁共能對位移的偏導(dǎo),即:
由文獻(xiàn)[2]推導(dǎo)可知,雙定子直線振蕩電機電磁力的表達(dá)式為:
因此可知,雙定子電機每單位電流產(chǎn)生電磁推力的大小與氣隙磁密Bg,每齒繞組匝數(shù)Nw,定子齒數(shù)N1以及永磁體寬度Wpm成正比。適當(dāng)?shù)脑O(shè)計各個參數(shù)的大小可獲得較大的能效比。
3雙定子直線振蕩電機機電系統(tǒng)建模
由于彈簧的使用,直線振蕩電機系統(tǒng)構(gòu)成了一個受迫振動系統(tǒng)。根據(jù)機械原理可知,其機械動力學(xué)模型可由F式表示:
m·a+c·v+k·x=F
空載時F-Fe,設(shè)Ke=2BgN1Wpm,早Fe-KeIe。又由于
因此 epm=Ke·v
由此可知,反電勢與速度成正比。
同理可知其驅(qū)動電路的數(shù)學(xué)模型:
加入補償電容后,數(shù)學(xué)模型可表示為:
4雙定子直線振蕩電機特性分析
從控制原理的角度來講,式(3)與(7)均可用二階傳遞函數(shù)來表示,是可以類同表示的。上述兩式分別可表示為:
從上式可看出,兩者傳遞函數(shù)雷同。因此,可將機械系統(tǒng)類比于電路系統(tǒng)進(jìn)行分析,從而建直一個機電系統(tǒng)得等效電路模型,對整個機電系統(tǒng)進(jìn)行綜合分析,從而得出各個物理量之間的關(guān)系。可將上述兩式作如下表示:
則機械系統(tǒng)等效阻抗為:
電路阻抗為:
眾所周知,電路系統(tǒng)存在諧振點,即電容提供的無功功率剛好補償電感負(fù)載需要的無功功率時的供電頻率,則 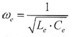 ,此時電路功率因數(shù)****,而機械系統(tǒng)共振點則為 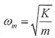 此時,Z e=R, 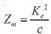 所以, 因此,此時電壓電流呈線性關(guān)系,相角差為零,功率因數(shù)****。而電電壓與位移幅值成正比,相角相差90度。
4 1雙定子直線振蕩電機諧振點性能分析
對(15)進(jìn)行微分求導(dǎo),得到最小值
即在電路與機械系統(tǒng)均達(dá)到諧振點且相等時,系統(tǒng)阻抗最小,結(jié)合(16)(17)可知,相同電壓下此時電流最小,位移****,且功率因數(shù)為l。但在實際系統(tǒng)中,由于電機主要應(yīng)用在壓縮機中,負(fù)載具有非線性特征,會對機械系統(tǒng)共振點產(chǎn)生影響,變負(fù)載時諧振點存在變化,因此,對于電路系統(tǒng)來說很難得到其準(zhǔn)確的補償電容,因此我們對于其未加補償電容時的特性作了深入分析,從而找到電機****工作點。由式(8)可知
傳遞函數(shù)伯德圖(具體參數(shù)值參見文獻(xiàn)[2],下同)如圖3所示。
由此可看出,在機械諧振頻率即當(dāng) 時,
此時,傳遞函數(shù)幅值****,即相同電流下得到的位移幅值****。由上述分析可看出,電機的效率與電路諧振頻率無關(guān),而僅與機械諧振頻率相關(guān)。因此,可將機械諧振點作為此時電機的****工作點。機械系統(tǒng)等效阻抗的頻域分析如圖4所示。
由上圖可知,在機械諧振頻率即當(dāng) 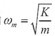 時, 即在機械諧振頻率下,產(chǎn)生相同反電勢需要電流最小,且機械系統(tǒng)功率因數(shù)為1,從而輸出有效功率****。而未加補償電容時機電耦合系統(tǒng)等效阻抗表達(dá)式為:
當(dāng)達(dá)到機械諧振頻率時,電路并未達(dá)到諧振頻率,因此整個系統(tǒng)并未達(dá)到諧振,主要是由于存在電感對于整個系統(tǒng)的影響。因此對其進(jìn)行了頻域分析,如圖5所示:
根據(jù)如圖分析,可知在機械系統(tǒng)達(dá)到諧振點時,傳遞函數(shù)達(dá)到****值,同時對于此時的功率因數(shù)進(jìn)行了解析計算,得到功率因數(shù)角為0.0027度,功率因數(shù)接近1,因此雖然由于電感的作用使得功率因數(shù)略有降低,但降低幅度非常小,基本可以忽略不計。因此,在未加補償電容時,機械諧振點無疑是電機的****工作點。
4 2雙定子直線振蕩電機電壓電流關(guān)系特性分析
由式(18)可知,在機電系統(tǒng)諧振狀態(tài)下,電壓電流應(yīng)為同相位成比例關(guān)系。但由于未加補償電容,電路系統(tǒng)未在諧振點上,而是存在偏移。因此,對于此時的電壓電流關(guān)系進(jìn)行了分析。此時:
由上式,電壓電流存在相位差,此相位差由于電感存在而造成。但經(jīng)過計算
發(fā)現(xiàn)電感的作用很小,即電壓電流相位差接近為0。
4 3雙定子直線振蕩電機電流位移關(guān)系特性分析
由式(17)可知,在諧振頻率下,電壓與位移幅值成正比,相角相差90度。但當(dāng)未加補償電容時,電壓與位移的關(guān)系為:
經(jīng)過計算,發(fā)現(xiàn)電感作用也較小,可近似于機械諧振時的特性。
5結(jié)論
從上述分析可以看出,在未加補償電容時,由于電路系統(tǒng)無法達(dá)到諧振點,因此,電壓電流不可避免存在相位差,功率因數(shù)達(dá)不到1。但系統(tǒng)仍然存在一個效率****的頻率點,這是由于機械共振系統(tǒng)作用的存在,由理論推導(dǎo)以及實驗驗證可知,在機械共振頻率下系統(tǒng)的效率****,同等電壓F,電流最小,位移****,功率因數(shù)接近l。
同時,對于電壓與電流關(guān)系特性,電壓與位移關(guān)系特性進(jìn)行了分析以及解析計算,發(fā)現(xiàn)電感對于系統(tǒng)影響較小,可將機械諧振點作為機電共振點近似進(jìn)行分析。
綜上所述,在難以對于控制電路進(jìn)行有效的無功補償?shù)臈l件下,將機械共振點作為電機的工作點是****選擇。
參考文獻(xiàn)
11l 葉云岳直線電機原理與應(yīng)用[M]機械工業(yè)出版社,2002
[2] 夏永明新型雙定子直線振蕩電機的研究[D]浙江火學(xué)博士論文,2007 |