通過上述分析可知,不同性質的負載具有不同的特性,而電動機也有其自身的特性:為了使系統能夠可靠穩定的運行,合理選配電動機的機械特性與負載機械特性是至關重要的。
為了分析方便,習慣上將電動機的機械特性曲線n=f(TM)和生產機械特性曲線n=f(TL)畫在同一個.T-n坐標平面上,如圖2.9所示,
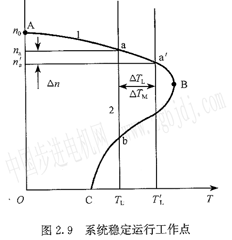
圖中曲線1為電動機的機械特性.曲線2為負載機械特性(恒轉矩型)。穩態時系統應處于勻速運動狀態.此時電動機軸上的拖動轉矩,TM和折算到電動機軸上的負載轉矩TL大小相等,方向相反.相互平衡。從T-_n坐標平面上來看,這意味著電動機的機械特性曲線和生產機械特性曲線必然有交點,此交點即為拖動系統的平衡點.如圖2.9中的交點a和b。
交點a和b是否都是系統穩定運行點呢?先來分析交點a的情況。實際的系統在運行中總會出現干擾,如電源的波動或負載的變化.現假設負載轉矩突然增加了△TL,則TL變為T′L,這時電動機來不及反應,轉速仍工作在原來的a點,其轉矩為TM,于是TMTL迫使電機加速.轉速n上升,系統重新回到原來的運行點a穩定運行;反之,若TL突然減小,n上升,當干擾消除后,也能回到a點穩定運行,所以a點是系統的穩定工作點。現在再來分析b點的情況,在b點運行時,若TL突然增加,n要下降,隨著n的下降TM要進一步減小,直至n等于0,電動機停轉;反之,若TL突然減小,n上升,隨著n的上升TM要進一步增大,促使n進一步上升,直至超過B點進入AtB段的a點工作。所以,b點不是系統的穩定平衡點。由此可見,對于恒轉矩負載,電動機的n增加時,必須具有向下傾斜的機械特性,系統才能穩定運行,若特性上翹,便不能穩定運行。
從以上分析可以得到機電傳動系統穩定運行的充分必要條件:
(1)電動機的機械特性曲線和生產機械的特性曲線有交點(即拖動系統的平衡點)。
(2)當轉速大于平衡點所對應的轉速時,應有TM<TL;而當轉速小于平衡點所對應的轉速時,TM>TL。
只有滿足上面兩個條件的平衡點,才是拖動系統的穩定平衡點,即只有這樣的特性配合,系統在受外界干擾后,才具有恢復到原平衡狀態的能力而進入穩定運行。
|