執行電動機選擇的基本依據伺服系統設計通常從選擇執行電動機開始。作為伺服系統的執行元件,應能方便地實現連續地、平滑地、可逆調速,對控制信號反應快捷,才能保證整個系統帶動被控對象按所要求的規律運動。
伺服系統應看作是被控對象的一個組成部分,執行電動機是伺服系統的一個重要組成部分,同時又要它驅動被控對象,因此它是伺服系統與被控對象相聯系的一個關鍵部件。執行電動機必須適應被控對象工作的特點與環境條件,它的機械結構尺寸、安裝固定方式,必須與被控對象緊密配合,以求得總體的合理配置,便于安裝調整,便于使用維護。這些都關系到執行電動機的選擇。在伺服系統應用的許多場合,要想改換別種類型的執行電動機,常會遇到機械結構、體積重量、使用環境條件、電源配備的種類等方面的限制,使設計難以實現。
可用作伺服系統執行元件的電動機種類很多,從大的類別看:有直流伺服電動機(他激的或承磁的)、直流力矩電動機、直流無刷電動機、兩相異步電動機、三相異步電動機、滑差電動機、同步電動機、各種步進電動機等等。由于它們調速方法不同、所需電源種類不同、驅動它們運轉的功率放大裝置更是多種多樣,因而它們的機械特性、調速特性、過載能力、線路的復雜程度、驅動功率的大小,以及構成系統的總成本,都各不相同,需要認真地具體分析比較來確定。
選擇執行電動機不能只停留在確定電動機的類別及其控制方式上,還必須確定具體型號與規格,需要作定量的核算。為此,要根據被控對象的運動形式(旋轉或直線運動),運動的變化規律,運動負載的性質和具體數量,運行工作體制(是長期連續運行或短時運行或間歇式運行),結合系統的穩態性能指標要求,作定量的分析。
伺服系統帶動被控對象運動,常常很難用簡單的數學表達式來描述,為便于工程設計計算,需作合理的簡化,首先應將被控對象運動負載作必要的典型分解,以轉動形式為例,常見的典型負載有以下幾種:
1)干摩擦力力矩Te=| TC| signΩ式中,Ω表示負載轉動的角速度(rad/s);sign為符號函數。
2)慣性轉矩Tj=jε式中,j為負載轉動慣量(kg·m?)ε為負載角加速度(rad/s?)。
3)粘性摩擦力矩Tb=CΩ式中,C為粘性摩擦系數(N·m·s)。
4)重力力矩TG=Gl式中,G表示負載重量(N);L負載重心垂線到轉動中心的距離(m)。
5)彈性力矩TK=KθM式中,K為扭轉彈性系數(N·m/rad);θm為負載轉動角度(rad)。
6)風阻力矩Tt=fΩ式中,f為風阻系數(N·m·s?)盡管伺服系統的負載特性多種多樣,其中大多數系統可用Tc和Tj兩種組合表示,有的需三種或多種典型負載的組合來表示。
以上典型負載與其運動參數(角速度或角加速度或角度)有關,如果被控對象的運動有規律,其角速度Ω(t)、角加速度ε(t)、角度θm(t)能用簡單的數學形式來表述,則定量分析系統負載的大小很方便。但多數被控對象的運動形態是隨機性的,很難用簡單的確定的格式來描述,工程上采取近似方法,或選取幾個有代表性的工況作定量分析計算。如長期運行時執行電動機的發熱狀態,短時超載或系統極限運行時執行電動機的承受能力,根據對系統動態性能的要求檢驗執行電動機的響應能力等。
顯然,被控對象的運動是與執行電動機的運動同時進行的。執行電動機除了要克服被控對象所形成的負載外,還必須克服電動機自身的干摩擦力矩Trc(N·m)和電動機轉子的慣性轉矩Jrεr[式中,Jr(kg-m?)為電動機轉子轉動慣量,εr(rad/s?)為電動機轉動角加速度]。當執行電動機與被控對象之間有變速傳動裝置時,還需要考慮傳動比i、傳動效率η和傳動裝置的等效轉動慣量JP(kg·m?)等因素被控對象的運動參數及負載特性需由用戶提出,而電動機的特性及其技術參數由生產廠家推出的產品目錄來提供。但電動機的種類多、型號多、生產廠家也多,所提供的產品技術參數也不一致。所用量綱也不統一,因此選執行電動機作定量計算時,必須作相應的換算。
例如LY系列永磁式直流力矩電動機產品目錄,列出電動機的輸出參數有:峰值堵轉力矩Tmb1****空載轉速nmo連續堵轉力矩Tcb1;對應的電動機輸入參數有:峰值堵轉電流Imb1和電壓Um,連續堵轉電流Icb1和電壓Uc;電動機自身的參數有:電勢系數ce,轉子轉動慣量JT,電磁時間常數Ti。
需要指出的是:其中nmo是電樞電壓為Um時電動機的實際空載轉速,并不是理想空載轉速njonmo和Tmb1可以決定電壓為Um時電動機機械特性,并可求出電動機自身的摩擦力矩Trc如對于90LY54系列電動機,它的技術參數:Um=48V,Imb1=1.5A,nmo=450r/min,Icbl=O 86A,UC=27.4V,Ce=0.096V/(r/min),ti=3ms,Tmb1=14kg·Cm=0,14×9.8=
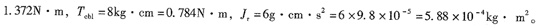
將Um、Ce代人式(4-1)得
nio=500r/min再由式(4-2)得
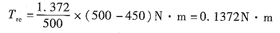
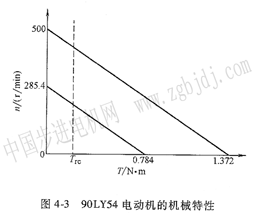
連接nio和Tmb1直線,如圖4—3所示是電壓為Um的機械待性,它代表該電動機特性的極限,在橫坐標Tcbl點作平行于第一條機械特性的平行線,即得電壓為Uc時的電動機機械特性,它的空載轉速no為
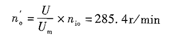
這兩條機械特性就是電動機定量計算的依據。
此外,直流力矩電動機電樞電阻Ra為

電動機的反電勢常數Ke(V.s)為對應90LY54電動機,其Ra=32Ω.Ke=0.9168V·s,電磁轉矩常數K=0.9168N.m/A,即Km的數值等于Ke但量綱應是N-m/A。這些數據對于進行定量分析,建立系統動態數學模型都是重要的、必需的。
例如SZ系列直流伺服電動機的技術數據,產品手冊上給出電動機的輸出參數有額定轉矩Tnom額定轉速nnom、額定功率Pnom,輸人參數有電樞額定電壓unom、額定電流,Jnom、激磁電壓Uf和激磁電流if;電樞轉動慣量Jr,其他參數需要用以下關系估算:
電樞電阻

電樞電感

式中,np為電動機磁極對數。
電勢常數

轉矩常數

在ZK型封閉式直流伺服電動機的技術數據中,有額定功率Pnom(kW)、額定電壓

轉子轉動慣量

電動機自身的摩擦力矩Trc可以用下式估算:

在sL系列兩相異步電動機的技術參數中,有電動機輸人參數:頻率,(Hz)、激磁電壓uf(V)、額定控制電壓unom堵轉電流,Ib1(A)、每相輸入功率Pφ(w);電動機輸出參數有額定輸入電壓Pnom(w)、空載轉速no(r/min)、堵轉轉矩Tbe(g·cm);電動機自身參數有極對數P、電動機時間常數Tm(s)。
兩相異步電動機自身摩擦力矩很小,計算時可忽略。其額定轉矩Tnom=1/2Tbe×9.8,額定轉速

電動機轉子轉動慣量
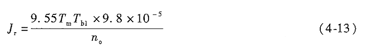
從產品手冊中所列數據可看出:兩相異步電動機的體積不小而輸出功率小,只適于功率很小的場合。但由于控制線路簡單,構成系統的成本低,仍應用很廣泛。
可供伺服系統用作執行元件的直流電動機的類數很多,其控制線路也比較簡單,加上直流電動機的調速特性線性化、實現可逆調速很方便,過載能力較大,因而在伺服系統中得到廣泛的應用。
三相異步電動機作為伺服系統執行元件還是近年來才出現,三相異步電動機本身成本低,性能穩定,便于維護,為獲得較寬的調速范圍,需采用變頻調速等較復雜的控制線路,目前用異步電動機構成伺服系統的總成本比直流伺服系統要高。但隨著電子產品價格的不斷下降,尤其是在中等功率特別是大功率的應用場合,交流伺服系統有逐漸替代直流伺服系統的趨勢。
|