0 引言電動車的關鍵技術之一是電機驅動系統的設計,包括電機的選擇與控制器的設計。基于系統成本及可靠性等方面的考慮,感應電機驅動系統具有一定的優勢。目前高性能的感應電機控制方法有磁場定向矢量控制和直接轉矩控制等幾種。
傳統的轉子磁場定向控制法對電機參數有較強的依賴性,而用于電動車的電機,其功率密度大,工作環境惡劣,電機參數在運行時變化較大,這就限制了磁場定向方法的使用。為此,近幾年出現了多種在線參數辨識方法,其中最為典型的是卡爾曼濾波器方法。雖然在理論上這些方法是可行的,但它們往往運算量較大,不利于進行實時控制;另外參數辨識的精度與信號檢測的精度相關,要求系統具有較高的電流、電壓、轉速檢測精度。本文對轉子磁場定向控制法進行了深入研究,采用了一種對感應電機參數變化具有較好魯棒性的控制方法。該方法運算量小、控制精度較高、對電機參數的變化不敏感,能較好地滿足電動車用高速電動機的動靜態性能要求。
1 矢量控制方法分析對感應電動機的矢量控制一般采用轉子磁鏈定向的方式。該方法中需要對轉子磁鏈進行估算。
通常的磁鏈觀測器大多利用電流模型完成。電流模型的狀態方程為:
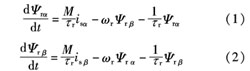
式中,ψrα、ψrβ分別為轉子磁鏈在靜止坐標系α一β下的分量,isαis β分別為定子電流在靜止坐標系α一β下的分量;ωr為轉子機械角速度;M、τr分別為互感和轉子時間常數。
由式(1)及式(2)可知,轉子時間常數的變化將影響磁鏈的計算結果,影響對轉子磁鏈方向的準確 跟蹤,若控制系統中缺乏針對電機參數變化的在線辨識控制算法,將降低系統的控制效果,嚴重時會引起系統的振蕩。為減少電機參數變化對控制系統的影響,本文采用如下磁鏈觀測模型:
 
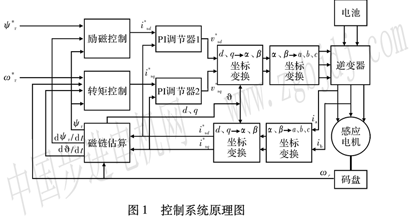
控制系統的工作原理如圖1所示。圖1中虛框里的為算法的核心,其中勵磁控制部分由式(3)完成,轉矩控制部分由式(4)完成,磁鏈估算部分由式(5)和式(6)完成。
2 仿真分析
本文利用Matlab進行了仿真。仿真所用的電機參數為:額定功率37.3 kW,額定頻率50 Hz,額定線電壓3 80 V,定子電阻O.087,轉子電阻O.228 Ω,定子電感O.8 mH,轉子電感O.8 mH,極對數為2。系統的給定負載轉矩為70 N·m,給定轉速為1 OO r/min,給定磁鏈為O.96 Wb。
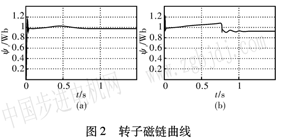
圖2為電機起動過程中轉子磁鏈ψr的變化曲線。其中圖2(a)為轉子時間常數正常條件下的仿真結果,圖2(b)為轉子時間常數減小一半時的仿真結果。在電機達到穩態時,圖2(a)中ψr=O.96Wb,圖2(b)中ψr=O.92 Wb。此時磁鏈ψr僅僅下降了4.2%,說明電機的穩態磁鏈ψr受轉子時間常數的影響較小。
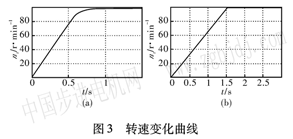
圖3為電機起動過程中電機轉速n的變化曲線。其中圖3(a)為電機轉子時間常數正常條件下的仿真結果,圖3(b)為轉子時間常數減小一半時的仿真結果。通過圖3可以看到:轉子時間常數的不同,會影響電機轉速的變化率;正常情況下,由于磁場定向的方向準確,電機的動態響應速度快,使得電機的轉速提升非常迅速。盡管轉子時間常數的變化影響了動態響應速度快,但電機達到穩態時的轉速未受影響。仿真結果說明,電機穩態時的轉速基本不受轉子時間常數的影響。
3 實驗研究
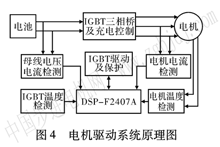
本文將上述控制方法用于電動車的感應電機控制系統中。系統所用的籠型三相感應電機的參數為:額定輸出功率23 kW,額定輸入線電壓1 90 V,額定電源頻率200 Hz,極對數2,額定轉速6 000 r/min,轉子電阻O.O 11 9508 Ω,轉子漏抗O.1 9 1 763 Ω,定子電阻O.O 1 24973 Ω,定子漏抗O.0914579 Ωo控制系統以DSP-F2407A作為控制核心,如圖4所示。以下實驗波形中的數據是在電機空載情況下通過DSP采集的,經繪圖軟件處理后形成了圖示曲線。
在實際電機長期運行過程中,要保持其轉子時間常數不變是不可能的。為了盡量減小溫升的影響,以下實驗波形是在電機繞組未發熱的短時間內測得的,可以近似認為在這段時間里轉子時間常數是不變的。由于實驗條件所限,實驗結果均為電機空載情況下的特性。
由于電機轉子是鼠籠式的,實驗時無法改變電機的真實轉子時間常數,只能人為地改變電機模型中用于計算的時間常數,但該時間常數變化產生的控制效果可間接地體現實際時間常數變化引起的控制結果。由于實際電機在運行過程中,其轉子電阻會有所變化,可能使計算結果與實際值之間存在一定的誤差,但該誤差的影響較小。
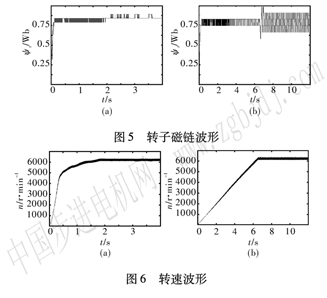
圖5為電機起動過程中電機轉子磁鏈的變化曲線,圖6為電機起動過程中電機轉速的變化曲線。
其中圖(a)為電機轉子時間常數正常條件下的實驗波形,圖(b)為參與計算的轉子時間常數減小一半時的實驗波形。
通過圖5及圖6中兩種條件下的波形對比可以看到,實驗結果與仿真結果基本一致,從而說明本文采用磁場定向矢量控制方法是有效的,它對電機參數的變化具有較好的魯棒性。
4 結 語
由于電動車用感應電動機具有高功率密度、高轉速等特點,當采用一般的磁場定向矢量控制方法時,存在難以克服的困難:系統性能對轉子時間常數變化敏感,而轉子時間常數又變化過大,這將導致系統性能不穩定。本文所采用的電機模型可降低控制系統對轉子時間常數的依賴性。仿真和實驗結果表明,本文所用方法可使控制系統具有較好的穩定性,可滿足電動車用感應電機驅動控制系統的技術要求。

|