摘要:設計了應用于半導體封裝設備金絲球邦定機的高速高精度直線電機x-Y平臺控制器,以達到高速、高精度響應,以及在外界干擾和參數不確定性因素影響下的魯棒性。通過對PI控制器、PDF控制器和PDFF控制器的性能比較,選擇PDFF作為速度環控制器、PlD作為位置環控制器的雙環控制架構。根據降階的系統模型、利用基本cRs算法對控制器參數進行優化。仿真和實驗結果證明,該控制方案具有良好的響應性能和魯棒性,加速度可以達到5 g,調整時間為4ms以內。
關鍵詞:直線電機;參數辨識;PDFF控制器;cRs算法;實驗
O 引 言
直線電機驅動系統由于減少了中間的非線性傳動環節,能夠很好地滿足現代微電子封裝技術高速高精度的發展需求。對于直線電機驅動的機電運動控制系統的建模,國內外許多學者都進行了相關的研究,并取得了顯著的成果。高速高精度系統呈現非線性、高階次、多變量、快時變、強耦合等特點,因此這類系統的模型比較難以建立,丁漢等利用各種動力學理論和控制理論對此類系統的建模進行_,深入的研究。shigeru Futa—mi等則利用動力學行為的計算機仿真與牛頓一歐拉法相結合的方法對系統進行建模,研究由交流直線電機驅動的采用滾珠導軌的精密定位乎臺的微動力學問題,并根據其微動力學特性,分別在平臺粗定位和精定位時實施有效地控制。M.Jouaneh等利用參數辨識法,建立了x—Y平臺的動力學模型,并利用頻率響應試驗數據所描述的動力學特性來建立數學模型,在此基礎上設計了帶有PID閉環控制器和切比雪夫低通濾波器的控制器。所設計的閉環控制系統的穩定時間是開環系統的1/3。本文針對danaher PLA_rJNuM(DDL)ILl8一075直線電機系統進行系統辨識得到高階模型并進行降階處理,然后根據所得低階模型設計H、PDF、PDFF速度換控制器,通過對比選擇PD.FF控制器作為速度環控制器,位置環控制器采用PID控制器,并通過cRs對各個控制器參數進行
整定。
1模型辨識
本文通過黑箱模型對系統進行辨識。假設系統的輸入μ(t)、輸出y(t)用線性差分方程表示
y(t)+a1y(t一1)+,…+any(t一n)=b1u(t一1)+,…,+bmu(i—m)
傳遞函數模型為:
y(t)=G(g)u(t)+H(g)e(t)
由于B—J模型輸入和干擾不相關,所以本文采用B—J模型。該模型表達式為:
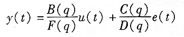
由于B—J模型輸入和干擾不相關,所以本文采用B—J模型。該模型表達式為:
系統辨識對于輸入信號的選擇主要有以下要求:
①在實驗期中,要求輸入信號的頻譜必須覆蓋系統的頻譜并能夠充分激勵系統的所有模態。
②保證輸入信號對系統的正負向擾動機會均等。定義擾動因子為:
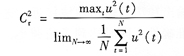
擾動因子越小,系統辨識結果越準確;可以看出,其最小值為l。
由于M序列含有豐富的頻率成分,它的譜密度函數在各個頻率點上的幅值是相等的,而且其擾動因子為1,是良好的系統辨識輸入信號。對于直線電機系統,由于不存在對絲杠等低速元件的沖擊,M序列更為理想。
通過實驗,得到系統的位置響應頻率大約是200 Hz,但是系統在約350 Hz和700 Hz時表現出振動模態。為準確得到系統的低頻模型和振動模態,可取輸入信號截止頻率fm=10000Hz。按照香農采樣定理取Ts≤1/(3fm-4fm),得采樣周期Ts=2 5 kHz。
辨識得到被控對象的離散形式的傳遞函數為:
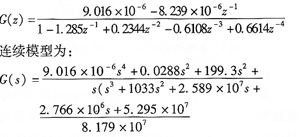
由于該模型不是真分式,需要對其進行降階處理,處理后的結果為
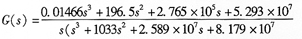
處理前后系統的bode如圖1所示。可以看出在1 kHz頻率范圍以內可以完全吻和,完全滿足需要。
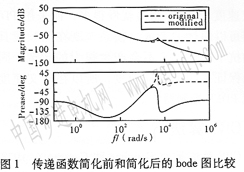
2控制架構選擇
本系統采用電流環、速度環和位置環三環控制架構,通常電流環不可調整。由于PLD控制器和P『控制器較常見,本文僅介紹PDF控制器和PDFF控制器。
PDF(Pseudo—Derivative—Feedhack)控制策略具有響應速度快、無超調、魯棒性強、抗干擾性能好等優點。PDF控制器和PI控制器很相似,都有積分環節和比例環節,不同的是PDF控制器使整個的誤差信號都通過積分環節,這使得PDF控制器比PI控制器響應速度慢,但是卻可以在PDF控制器中提高積分增益,從而使系統能夠更好的抑制低頻段的干擾,提高系統的魯棒性。PDF控制器的輸出為:
ICMD=(KvI∫(VPCMB-VFB)dt-VFBKv在PDF控制器加入前饋環節形成了PDFF控制器。該前饋環節是由比例增益KVER決定的。這一前饋使得在輸人命令在經過積分之前進入系統,從而系統的響應更加迅速。
同時PDFF控制器是對PI控制器的一種拓展,通過對PI控制器的算法的修改使超調減小,并允許低頻段具有很大的剛度。PDFF控制器的輸出為IcMD=(KVI∫(VPCMD-VEB)dt+KVFR VPCMD-VEB)KVPDF控制器和PI控制器都可以看做是PDFF控制器的特例,也就是KVFR取極限時的情況。當KVFR=1時,PDFF控制器變為H控制器。當KVFR=0時,PDFF控制器變為PDF控制器,而在0
控制器的優點,即PDFF控制器是PDF控制器和PI控制器的綜合體現。
可以看出PI控制器雖然響應速度較快,但如果將積分增益調得很高以使低頻段抗干擾能力增強的時候,則會使系統產生超調。相反PDF控制器則可以使系統在低頻段的抗干擾能力很強,但響應速度較PI控制器就慢很多,而采用PDFF控制器可以通過調節KVFR使系統既在低頻段具有很好的抗干擾性,又不會產生很大的超調,同時還可以保證系統的響應速度,所以在本文速度環上采用PDFF控制器。
3 cRs算法
cRs算法是由G0ucher和casares在1978年最早提出的算法,在獲得全局****解方面非常有效。
對于本課題所使用的PDFF+PID控制結構,用cRs算法尋找****解,是一種工業上可行的方案,并且能夠彌補早期的整定方法如Ziegler—Nich01s算法,極點配置等方法在快速性方面的不足。
cRs算法分為兩部分,第一部分應用撕裂算法減少了需要同時解決的等式約束,建立起一個有著特殊排列規律的矩陣,產生一系列可以計算未知數的規范,在必要的時候,可以同時解多組等式方程。該算法在奇異點處、非線性區域或者變量的雅可比矩陣接近奇異時都將會出現一些問題,但迄今這些問題在實際系統中都是很少遇見的。
在cRs算法的第二部分,cRs算法由一個用戶自定義的初始點開始搜尋****解,也可以自動產生一個切實可行的初始點。利用高斯準則對每個新點進行迭代,把標準偏差向量作為一個決策性向量的函數來計算。該決策性向量的上下限由一個參數k1決定(k1的默認值為1/3),通過解等式來驗證新點的可行性,并帶人不等式驗證,其中等式可利用修改過的牛頓拉夫申公式解出。當嘗試很多次都沒有結果時,標準決策性向量將會被減小,并與另一個參數k2相乘(k2的默認值為1/2)。嘗試的次數為ηena其中n為決策性變量的個數,ηe為第三個參數(ηe的默認值為25)。當一個能夠使目標函數更優的可行點被找到時,一次新的迭代就開始了,標準偏差函數的元素也就被更新了。收斂準則是基于目標函數和決策性變量對前面所定義準則的承受能力而定的。
當完成了一次成功的嘗試之后,標準偏差向量就被調整為:

此時得到的xi即為所求的參數。在式中經常取ε=O.001。本文選取超調量和調整時間作為參數整定的目標函數。
4仿真和實驗
(1)速度環仿真及實驗根據式(3)所得的系統模型,應用cRs算法以調整時間和超調量為目標函數整定速度環PDFF控制器的參數結果為KV=3 570,KVI=9 247,KVER=0.8系統以仿真曲線如圖2所示。同樣命令下的實際輸入輸出曲線如圖3所示。可以看出對于同一輸入,實際輸出和仿真輸出曲線接近,進一步證明了模型的準確性,同時達到了超調小,調整時間短的目標。
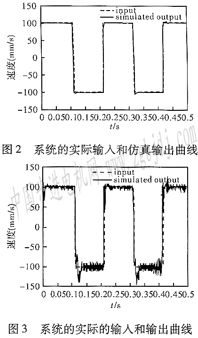
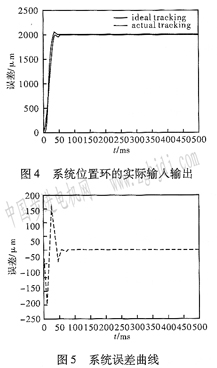
(2)位置環仿真及實驗對于含有PID控制器作為位置環的控制器全環控制架構,利用cRs算法以調整時間和超調量為目標函數對PID控制器的參數進行整定,得到的參數為:KP=9 049,Ki==6 269,Kd=190。
系統的實際輸入輸出曲線如圖4所示。誤差曲線如圖5所示。實際系統調整時間4ms,超調6%,達到要求。
5結論
PDFF控制器作為速度環控制器,既可以繼承PI控制器的快速性,又提高了系統的魯棒性,因而在對快速性和魯棒性要求很苛刻的高速高精度直線電機驅動平臺上具有很高的應用價值。在位置環PID+速度環PDFF控制架構下,采用CRS算法以超調量和調整時間為目標函數專系統控制器進行參數整定,得到****的控制器參數組合,以達到設計目標,彌補了傳統的整定方法在快速性上的不足,并消除了手動調整的繁瑣,很好的滿足了工業的需要。
