摘要:提出了一種扇形齒一凹槽結構的雙轉子模態轉換型超聲波電動機,它依靠扇形齒一凹槽結構將壓電陶瓷振子的縱振動轉換為齒的彎曲振動來驅動轉子旋轉。對電機有限兀模型進行了仿真分析,包括調節驅動頻率、計算齒振幅轉換比、分析裝配誤差影響、計算定子表面質點軌跡:并通過建立定轉子接觸的簡化模型,對電機在諧振狀態下的輸出力矩進行計算最后制作了尺寸為φ8mm×10mm樣機,經實驗表明,電機連續運轉性能良好.在驅動電壓為135 V時,轉速町達475 r/min:
關鍵詞:超聲波電動機;模態轉換;雙轉子;有限元:接觸
O引 言
超聲波電動機是利用壓電材料的逆壓電效應制成的新型致動器,由定子、轉子以及施加預壓力的機構等部件構成。在壓電陶瓷上施加超聲頻交變電壓可以在定子表面產生超聲振動,通過定子與轉子之間的摩擦力驅動轉子運動
超聲波電動機已經成功地用于相機自動調焦、設備精密定位、以及汽車、航天、機器人和醫療設備中。近幾年,隨著微機械、微電子的陜速發展,對微型電機的需求越來越多:由于超聲波電動機的結構多樣、靈活,在微型電機市場中更有發展前景一
模態轉換型電機是一種針對大力矩、單一旋同等特殊需求的超聲波電動機,依靠模態轉換機構來
產生能驅動轉子旋轉的振動模態一般情況下,作為驅動力源的振動采用機電轉換能力較高的縱振子
來完成,所以模態轉換型電機的轉換效率較高,適于大功率輸出.
模態轉換型電機的主要部分是振動模態的轉換機構和定子對轉子的撥動機構.由于模態轉換型電
機均為單模態驅動,因此其定子驅動端軌跡未必就是一個橢圓,可能是橢圓的一種變形。而正因為這種變形的軌跡,才反而使轉子與定子之間的相對滑動減少,提高了實際效率。
1985年kkio Kumada提出了一種定子上具有單梁結構的模態轉換型電機,可以使壓電堆的縱向
振動轉化為梁的扭轉振動。
因為單梁與轉子接觸不穩定,噪聲大,所以清華大學聲學實驗室對AkioKumada的設計做了改進
設計定子上具有三梁結構的電機’,這種設計有效地降低了噪聲和提高了穩定性,但缺點是加工工藝復雜:于是1996年又設計了一種定子上具有雙梁結構的電機。,通過壓電陶瓷堆的縱振動來激發蔗子上雙梁的某種低頻彎曲振動,來推動轉子旋轉。
陜西師范大學在定子上安置梁狀振動片來實現模態轉換,并研究了振動片和轉子摩擦接觸的運動軌跡和動力學特征,指出振動片與轉子軸線平行時摩擦力****,電機動力****。浙江大學研制了一
種斜齒駐波型超聲波電動機,在定子表面沿周向分布有50°~70°的斜齒,該電機借助于定子表面的斜齒與轉子的相互壓緊,使斜齒端面質點產生橢圓運動,實現轉子單方向旋轉運動。
本文提出了一種扇形齒一凹槽結構的雙轉子模態轉換型超聲波電動機,建立了電機的有限元模型,對其進行了仿真分析,并通過建立定轉子接觸的簡化模型,對電機在諧振狀態下的輸出力矩進行了計算。
1電機的基本結構和工作原理
該電機照片和它的定子結構如圖1所示。定子金屬體上設置四個扇形齒一凹槽用于模態轉換。電
機工作時,給壓電陶瓷振子施加單相正弦交變電壓,通過扇形齒一凹槽的模態轉換將振子的縱振動轉化為齒的彎曲振動,形成駐波橢圓運動,驅動轉子旋轉,如圖2所示。
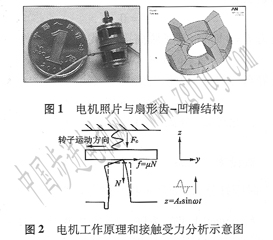
圈2電機工作原理和接觸受力分析示意圖
已有的斜齒狀結構運行時齒容易斷裂,相比之下,扇形齒狀結構剛度較高,不易斷裂,更利于加工。在齒的足部刻有凹槽,使得齒在凹槽一側的局部剛度變小,齒更容易向凹槽方向彎曲,有利于增大齒的彎曲振幅。
目前已有的模態轉換型電機均為單轉子結構。為了進一步提高輸出效率,本文采用了雙轉子結構,在定子兩端均有帶扇形齒凹槽的金屬體和轉子。電機由壓電陶瓷縱振子、振子兩端金屬體、兩端轉子、轉軸以及預緊機構組成。
定子的金屬體設計有內螺紋,通過帶孔螺桿使兩端金屬體夾緊中間的壓電陶瓷縱振子,形成郎之
萬的夾心結構,避免了采用粘結劑帶來的粘結劑老化等問題。軸穿過螺桿孔,用螺母擰緊彈簧給兩端轉子施加預壓力,將其壓緊到齒的端面。
2電機仿真分析
2 1電機定子的驅動頻率調節
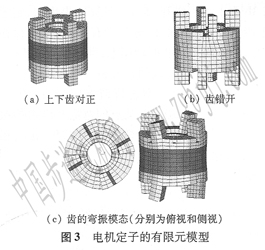
電機定子的機電耦合有限元模型如圖3所示。其中兩端藍綠色部分是齒狀結構,材料是45號鋼,
中間紫色部分是兩片普通壓電陶瓷片。
該模型存在每個齒彎曲方向一致的振動模態,如圖3c所示。電機的驅動頻率應取為稍低于該模
態的頻率(若高于該頻率,齒則相當于隔振彈簧)。但因電機采用了縱振子為驅動力源,為了增大振幅,應盡可能調節齒的彎振模態頻率使之與定子的縱振動模態頻率一致。
定子縱振動模態頻率主要取決于定子的高度,因研究需要,其直徑和高度均為8 mm,因此定子縱
振模態頻率是固定值。對齒彎振模態頻率影響較大的參數為齒的高度,所以只計算齒的彎振模態頻率隨齒高的變化。
計算結果如圖4 所示。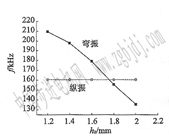
可以看出,隨 齒高的增加,齒彎振模態頻率逐漸減小, 而定子縱振模態頻率 基本保持160 kHz不 變。當齒高為l.8 mm圖4改變齒高對定子頻率的影響時,齒彎振模態頻率與定子縱振模態頻率幾乎相等,因此將齒高定為1.8 mm。
2 2齒的振幅轉換比計算
定義齒的彎振模態的振幅轉換比為c=B分之A中A為齒端面某點的彎振幅,B為齒底部的某點的
縱振幅,A和B的比值能夠反映扇形齒一凹槽結構的振幅轉換倍數。
根據齒的結構,轉換比c受齒高影響****,計算結果如圖5所示。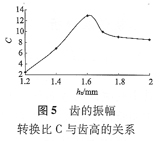
由圖5可知,當齒高在1.2 mm
到1.6 mm范圍內逐漸增加時,c大幅上升;當齒高大于l.6 mm時,c平緩下降,原因是當齒高過高時,齒的隔振效應變強,不能有效地將縱振轉換為齒的彎振。c****值為13倍,說明該種模態轉換結構有優良的將縱振動轉化并放大為齒的彎曲振動的能力。
2.3上下齒角度差對電機頻率的影響
在實際裝配時,定子上下端面的齒會錯開一定的角度。因此建立上下齒錯開的定子有限元模型(圖3b中上下齒錯開15°)。計算結果表明,定子的上下齒錯開對電機的模態并沒有影響,依然存在每
個齒彎曲方向一致的振動模態,且諧振頻率不改變。
2.4定子表面質點運動軌跡分析
通過對有限元模型進行諧響應分析(電壓20V),可以計算出齒端面上某點的彎振和縱振的振幅
以及相位。計算結果為:彎振幅為1.91μm、相位50.7°,縱振幅為O.5μm、相位61.O°。根據振幅和相位可以計算出該點在一個周期T內的軌跡,如圖6所示。可以看出,齒的運動軌跡是一個壓扁的圖6定子齒邊某點的運動軌跡傾斜橢圓。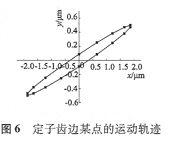
3電機定轉子接觸分析和定子輸出力矩仿真
計算
定子輸出力矩計算時需考慮定轉子的接觸受力情況。盡管已有不少扭縱駐波超聲波電動機的接觸
模型,在此依然根據本電機材料特點和裝配結構做如下簡化假設:通過一個理想的輕彈簧壓在轉
子上施加預壓力,彈簧的彈性系數為k,初始狀態的彈簧變形量為c。考慮到電機可能水平放置,忽略重力。定子和轉子的剛度系數遠大于預緊彈簧,因此定子的齒和轉子接觸時,忽略定子和轉子相互擠壓造成的形變。忽略水平和垂直方向運動的耦合。定子振動是理想的正弦波,其波形與頻率不受與轉子接觸的影響。接觸模型如圖2所示。
在定子做縱振動的一個周期T內,從零時刻開始,齒同時做y軸負方向的彎曲振動和Z軸正方向
的縱振動,齒端面傾斜,僅有一條邊與轉子相接觸并撥動轉子旋轉。假設轉子對該接觸邊的壓力為F,轉子對齒的摩擦力為f0由摩擦力公式有:
f=μF (1)
設Fc為彈簧對轉子的預壓力,z為定轉子接觸邊的縱向位移。假設接觸邊的縱振幅為Az,那么t
時刻該邊縱向位移z=A,sinωt.因此預壓力為:
Fc=一k(z+c)=- k(Azsin ωt+c) (2)
共有四個齒同時對該轉子作用,設F′為F的反作用力,即齒對轉子的支持力,設m為轉子質量,a
為轉子加速度,轉子的受力方程為:
4F′+Fc=ma (3)
定轉子接觸時加速度相同,那么:
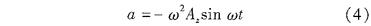
代入式(3)求得轉子對齒接觸邊的壓力為: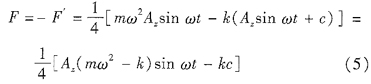
轉子對齒的摩擦力為:
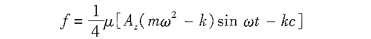
初始狀態:
f=0 (6)
壓力F=O時,定轉子脫離接觸,得到分離條件:
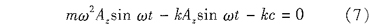
設靜態時的預壓力****值為Fc0式(7)化為
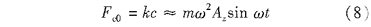
由此可知,分離時間f與靜態時預壓力Fc0有關。

態,在實際運行中,如果預壓力過小,那么定轉子便過早分離,驅動效率不高;如果預壓力過大那么定轉子便不存在分離,齒會阻礙轉子旋轉。
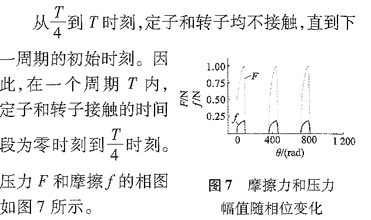
從以上推導可以看出,當電機運行時,定子對轉子的驅動力以及預壓力Fc的值均是波動的,并且頻
率和相位均與齒接觸邊的縱振動一致。由于齒的縱振幅AZ遠小于彈簧初始形變c,因此Fc波動的幅值
相當小,有時可以認為預壓力基本不變。而驅動力波動的幅值與靜態預壓力成正比,并目.是間斷的,理想情況下存在于0到四分之T周期內。
由于轉子的慣性轉矩等因素,轉子的輸出力矩并不象驅動力一樣是間斷的,而是在某個固定值附
近波動,其波動的頻率和相位同定子縱振動一致:
根據以上模型和推導,可以簡單的用壓力F和摩擦力f來代替轉子對定子的全部作用,計算定子對轉子的****輸出力矩,從而避免復雜的接觸計算。
在有限元分析里,力可以直接加在單元上,故將有限元模型每個齒的定轉子接觸邊上所有單元均施加壓力FS和切向摩擦力FS,如圖8所示。
假設壓力F和摩擦力f沿齒的接觸邊平均分布,模型中單個齒的接觸邊上有5個單元,有:
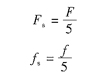
將電壓固定為60 v、驅動頻率為150 kHz,計算齒彎振振幅隨摩擦力fS和壓力FS的變化,計算結果如圖9所示。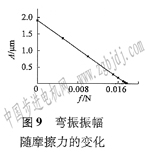
從圖中可以看出,隨著摩擦力fS的增大,齒的彎振振幅線性減小,當摩擦力fS為0.018 N時,齒的彎振振幅接近零,此時摩擦力即為齒驅動轉子的****摩擦力。單個齒對轉子的輸出轉矩為接觸邊上五個單元的轉矩之和,有:
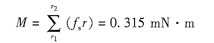 由于電機是雙轉子結構,一共有8個齒,總的輸出力矩: 由于電機是雙轉子結構,一共有8個齒,總的輸出力矩:
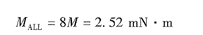 由于計算時電壓為60 v,而實際電壓可以加到200V左右所以該電機的輸出力矩理論上應該大于3 mN·m。 由于計算時電壓為60 v,而實際電壓可以加到200V左右所以該電機的輸出力矩理論上應該大于3 mN·m。
4實驗
最后制作的樣機尺寸為φ8 mm×10 mm,驅動頻率148 kHz,在該頻率下電機運行平穩,連續運轉性能良好。利用非接觸轉速測量儀對電機轉速隨電壓幅值的變化關系進行測試,測量結果如圖lO所示。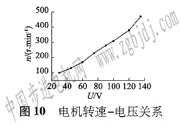
可以看出,隨著電壓的增大,電機轉速線性上升。當驅動電壓為135 V時,轉速為475 r/min。
5結語
本文提出了一種新型雙轉子模態轉換型電機,設計了定子上的扇形齒一凹槽模態轉換結構,并針對電機的有限元模型進行了仿真研究。仿真結果表明:
(1)當齒高為1.8 mm時,電機定子縱振動模態頻率和齒彎振模態頻率一致,有利于增大振幅。
(2)計算齒高對振幅轉換比的影響,該種結構的****轉換比為13倍。
(3)證明裝配時上下端面的齒錯開對定子的振動模態并無影響。
(4)計算出定子齒在自由諧振狀態下的運動軌跡,為一壓扁的傾斜橢圓。
(5)建立定轉子的簡化接觸模型,指出在電機運行時,其預壓力、定子對轉子的驅動摩擦力均與縱
振子的振動做同頻率同相位的波動。并根據模型計算出定子對轉子的****輸出力矩。仿真計算為實驗及以后進一步研究提供了理論參考。最后制作一臺尺寸為φ8 mm×10 mm樣機,經過實驗表明,電機運行平穩,連續運轉性能良好。在驅動電壓為135 v時,轉速可達475 r/min。

|