一、逆壓電效應(yīng)簡介
壓電效應(yīng)是在1880年由法國的居里兄弟首先發(fā)現(xiàn)的。一般在電場作用下,可以引起電介質(zhì)中帶電粒子的相對運動而發(fā)生極化,但是某些電介質(zhì)晶體也可以在純機械應(yīng)力作用下發(fā)生極化,并導(dǎo)致介質(zhì)兩端表面內(nèi)出現(xiàn)極性相反的束縛電荷,其電荷密度與外力成正比。這種由于機械應(yīng)力的作用而使晶體發(fā)生極化的現(xiàn)象,稱為正壓電效應(yīng);反之,將一塊晶體置于外電場中,在電場的作用下,晶體內(nèi)部正負電荷的重心會發(fā)生位移.這一極化位移又會導(dǎo)致晶體發(fā)生形變。這種由于外電場的作用而使晶體發(fā)生形變的現(xiàn)象,稱為逆壓電效應(yīng),也稱為電致伸縮效應(yīng)。正壓電效應(yīng)和逆壓電效應(yīng)統(tǒng)稱為壓電效應(yīng)。
超聲波電動機就是利用逆壓電效應(yīng)進行工作的,圖9 2所示為逆壓電效應(yīng)示意圖,進一步說明了逆
壓電效應(yīng)的作用。壓電體的極化方向如圖9-2中箭頭所示.當(dāng)在壓電體的上、下表面施加正向電壓.
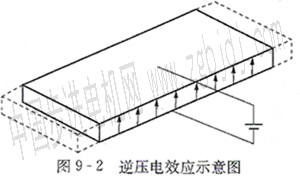
即在壓電體表面形成上正、下負的電場時,壓電體在長度方向便會伸張;反之,若在壓電體上、下表面施加反向電場.則壓電體在長度方向就會收縮。當(dāng)對壓電體施加交變電場時,在壓電體中就會激發(fā)出某種模態(tài)的彈性振動。當(dāng)外電場的交變頻率與壓電體的機械諧振頻率一致時,壓電體就進入機械諧振狀態(tài)。成為壓電振子。當(dāng)振動頻率在20kHz以上時,就屬于超聲振動。
二、橢圓運動及其作用
超聲振動是超聲波電動機工作的最基本條件,起驅(qū)動源的作用。但是.并不是任意超聲振動都具有驅(qū)動作用,它必須具備一定的形態(tài).即振動位移的軌跡是一橢圓時,才具有連續(xù)的定向驅(qū)動作用。
圖9-3所示質(zhì)點的橢圓運動示意圖,設(shè)定子(振子)在靜止狀態(tài)下與轉(zhuǎn)子表面有一微小間隙.當(dāng)定子產(chǎn)生超聲振動時,其上的接觸摩擦點(質(zhì)點)A做周期運動.軌跡為一橢圓。當(dāng)A點運動到橢圓的上半圓時,將與轉(zhuǎn)子表面接觸.并通過摩擦作用撥動轉(zhuǎn)子旋轉(zhuǎn);當(dāng)A點運動到橢圓的下半圓時,將與轉(zhuǎn)子表面脫離,并反向回程。如果這種橢圓運動連續(xù)不斷地進行下去.則對轉(zhuǎn)子具有連續(xù)的定向撥動作用。從而使轉(zhuǎn)子連續(xù)不斷地旋轉(zhuǎn)。因此,超聲波電動機定子的任務(wù)就是采用合理的結(jié)構(gòu),通過各種振動的組合來形成橢圓運動。
那么,怎樣才能形成橢圓運動呢?設(shè)有兩個空間相互垂直的振動位移ux和uy,均是由簡諧振動形成,振動角頻率為ω0,振幅分別為ξx和ξy,時間相位差為ψ即有

從中消去時間t,則有
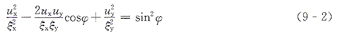
式(9-2)中,當(dāng)ψ=nπ(n=0,±l,±2.…)時,兩個位移為同向運動,合成軌跡
為一條直線;當(dāng)ψ≠nπ時,其軌跡為一橢圓,并且在ψ=nπ±π/2時為一規(guī)則橢圓。不同相位
差時的橢圓形態(tài)如圖9 -4所示。
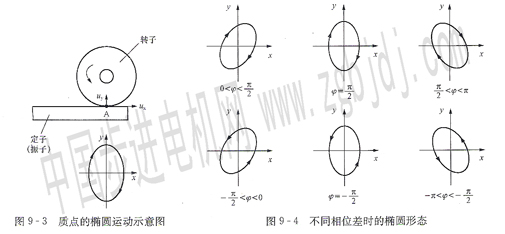
由此可見,相位差ψ的取值就決定了橢圓運動的旋轉(zhuǎn)方向.當(dāng)ψ>O時.橢圓運動為順時針方向,當(dāng)ψ 三、行波的形成及特點
上面討論的是一個質(zhì)點橢圓運動的作用。單靠一個質(zhì)點的橢圓運動還不足以推動轉(zhuǎn)子并驅(qū)動一定的負載,而應(yīng)該依靠一系列質(zhì)點的連續(xù)橢圓運動來推動轉(zhuǎn)子旋轉(zhuǎn),也就是說這些質(zhì)點需要進行行波眭質(zhì)的運動。根據(jù)波動學(xué)理論,兩路幅值相等、頻率相同、時間和空問均相差π/2的兩相駐波疊加后.將形成一個合成行波。
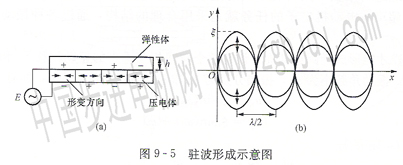
如圖9 5(a)所示,將極化方向相反的壓電體依次粘結(jié)在彈性體上.當(dāng)在壓電體極化方向施加交變電壓時,壓電體在長度方向?qū)a(chǎn)生交替伸縮形變,在一定的激振電壓頻率ω0下,彈性體上將產(chǎn)生如圖9-5(b)所示的駐波.其數(shù)學(xué)表達式為
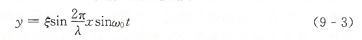
式中:χ為橫向坐標;y為縱向坐標;ξ為駐波波幅:λ為駐波波長。
設(shè)在彈性體上同時存在兩相駐波A和B,它們的頻率同為ω0.波幅同為ξ.波長同為λ并且在時間和空間上均相差π/2,即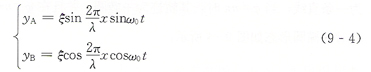
其合成為
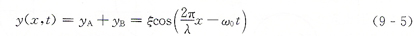
這是一個頻率為ω0、波幅為ξ、波長為λ的行波。
在環(huán)形行波型超聲波電動機中,定子上的壓電陶瓷環(huán)是行波形成的核心,它的電極配置如圖9—6所示,其中。+”、-”表示極化方向。壓電陶瓷片按照一定規(guī)律分割極化后分為A、B兩相區(qū),兩相空間排列相差π/2(1/4波長),并且分別施加在時間上也相差π/2的高頻交流電(E1和E2)A、B兩相分別在彈性體上激起駐波。兩相駐波疊加后,將形成一個沿定子圓周方向的合成行波,推動轉(zhuǎn)子旋轉(zhuǎn)。
壓電陶瓷片的厚度決定了在一定電壓下是否能夠起振,如果壓電陶瓷片太厚(大于1.5mm),則在通常情況下不易起振;如果壓電陶瓷片太薄(小于O.3mm),則在高頻諧振條件下,由于形變過大而容易發(fā)生斷裂,并且加工難度也會增大。另外,壓電陶瓷片的厚度對壓電振子的固有諧振頻率
影響較大,通常取其厚度為0.5~0.8mm。
由上可見.由兩個駐波疊加而形成行波,這在機理上與電機學(xué)中的旋轉(zhuǎn)磁場理論有諸多相似之處。由本書第四章知道,當(dāng)在單相繞組中通人單相交流電流時產(chǎn)生的是脈振磁場,如果有兩個匝數(shù)相同、空間互差90°電角度的繞組,當(dāng)在其中通人幅值相等、時間相位互差90°的對稱交流電流時,
所產(chǎn)生的兩個脈振磁場的合成就是一個圓形的旋轉(zhuǎn)磁場,旋轉(zhuǎn)磁場的轉(zhuǎn)向取決于電流的相序。在這里.彈性體中的駐波與單相脈振磁場相對應(yīng).而合成行波與旋轉(zhuǎn)磁場相對應(yīng)。將超聲波電動機的行波與交流電機的旋轉(zhuǎn)磁場聯(lián)系起來,有助于對行波型超聲波電動機工作原理的理解。
四、轉(zhuǎn)子運動速度
下面通過分析彈性體表面上任意一點的運動軌跡,來確定轉(zhuǎn)子運動的速度。
根據(jù)式(9-5),在任意時刻f,彈性體表面上某點P的縱向振動位移為

設(shè)彈性體的厚度為H,則P點的橫向振動位移為
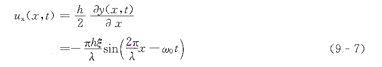
由式(9 6)和式(9—7),得

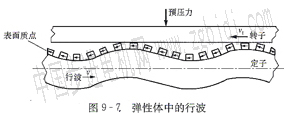
由此可見,彈性體表面上任意一點的運動軌跡為橢圓形,這種橢圓運動使得彈性體表面質(zhì)點對轉(zhuǎn)子產(chǎn)生連續(xù)的定向撥動作用.且轉(zhuǎn)子的運動方向與行波方向相反,如圖9-7所示(圖9—7中小箭頭表示彈性體表面質(zhì)點的瞬時速度)。顯然,如果改變激振電源的電壓極性,便可以改變轉(zhuǎn)子的運動方向。
根據(jù)式(9 7),彈性體表面質(zhì)點的橫向運動速度為
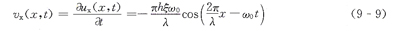
橫向速度的****值應(yīng)出現(xiàn)在行波的波峰或波谷處。此時的表面質(zhì)點沒有縱向速度,耳.橫向速度與行波方向相反(見圖9-7)。若定、轉(zhuǎn)子接觸面之間沒有滑動,則轉(zhuǎn)子的運動速度與波峰處質(zhì)點的橫向速度相等,其值為
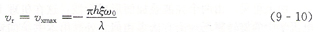
式中:負號表示轉(zhuǎn)子的運動方向與行波方向相反。
實際上,定、轉(zhuǎn)子接觸面之間的滑動是難免的,因此超聲波電動機轉(zhuǎn)子的實際運動速度總是低于式(9-10)的值。
設(shè)行波在定子彈性體中的傳播速度為υ由行波的基本特性可知
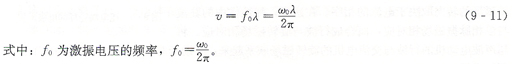
這樣,轉(zhuǎn)子運動速度又可寫為
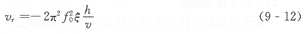
可見,在行波傳播速度υ為恒值的情況下,改變激振電壓的頻率f0可以快速改變轉(zhuǎn)速但存在一定的非線性。而改變激振電壓的大小,即改變行波的振幅ξ,也可以改變轉(zhuǎn)速。如果忽略壓電體逆壓電效應(yīng)的非線性,則轉(zhuǎn)速可以隨激振電壓做線性變化,這就是超聲波電動機變壓調(diào)速的特點。
五、工作特性
一般而言,超聲波電動機的工作特性與電磁式直流伺服電動機類似,電動機的轉(zhuǎn)速隨著轉(zhuǎn)矩的增大而下降,并且呈現(xiàn)一定的非線性。而超聲波電動機的效率則與電磁式電機不同,****效率出現(xiàn)在低速、大轉(zhuǎn)矩區(qū)域,圖9-8所示為超聲波電動機的工作特性。
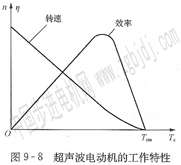
因此,超聲波電動機非常適合低速運行。總體而言,超聲波電動機的效率較低.這是它的一個缺點。目前。環(huán)形行波型超聲波電動機的效率一般不超過50%。
|