連續(xù)及采樣異結(jié)構(gòu)混沌同步控制
吳忠強(qiáng)1,鄺鈺1,湯輝2
(1燕山大學(xué)西校區(qū)電院工業(yè)計(jì)算機(jī)控制工程河北省重點(diǎn)實(shí)驗(yàn)室,河北秦皇島066004;2唐鋼煉鐵廠,河北唐山063000)
摘 要:研究了一類(lèi)畀結(jié)構(gòu)混沌全狀態(tài)同步控制問(wèn)題。分別以CoulleL系統(tǒng)與Rossler系統(tǒng)為目標(biāo)和響應(yīng)系統(tǒng),采用backstepping方法設(shè)計(jì)了保持兩系統(tǒng)之間所有狀態(tài)同步的連續(xù)時(shí)間控制器,為了把連續(xù)控制器更好地應(yīng)用到計(jì)算機(jī)采樣控制系統(tǒng)中,在連續(xù)控制器設(shè)計(jì)的基礎(chǔ)之上,基于采樣系統(tǒng)實(shí)用半局漸近穩(wěn)定理論,又進(jìn)行了采樣同步控制器的再設(shè)計(jì)研究。仿真結(jié)果證明了所設(shè)計(jì)的連續(xù)及采樣同步控制器的有效性,并進(jìn)一步表明所設(shè)計(jì)的采樣同步控制器,與由連續(xù)控制器直接離散化所得的控制器相比,具有更快的收斂速度,而且在保證系統(tǒng)穩(wěn)定的前提下還具有更寬的采樣周期選擇范圍?
關(guān)鍵詞:異結(jié)構(gòu);混沌;同步;采樣控制;反步法
中圖分類(lèi)號(hào):TP 273 文獻(xiàn)標(biāo)識(shí)碼:A
1引言
已成為非線(xiàn)性科學(xué)研究熱點(diǎn)的混沌控制與同步,在保密通信、醫(yī)學(xué)、生物等領(lǐng)域具有很大的應(yīng)用潛力和發(fā)展前景,現(xiàn)已提出的混沌向步方法中多數(shù)集中于同結(jié)構(gòu)混沌同步。異結(jié)構(gòu)混沌同步也正越來(lái)越多地受到人們的關(guān)注,有的異結(jié)構(gòu)同步只實(shí)現(xiàn)兩混沌系統(tǒng)間的某個(gè)對(duì)應(yīng)狀態(tài)的同步,本文以Coullet系統(tǒng)為目標(biāo)系統(tǒng),以Rossler系統(tǒng)作為響應(yīng)系統(tǒng),給出了一種保持兩系統(tǒng)間3個(gè)狀態(tài)分別同步的連續(xù)時(shí)間控制器Backstepping設(shè)計(jì)方法,并且通過(guò)仿真試驗(yàn)證明了控制器的有效性。
如果把按照連續(xù)控制理論所設(shè)計(jì)的控制器直接應(yīng)用到計(jì)算機(jī)采樣系統(tǒng)之中,采樣系統(tǒng)往往隨著采樣周期的增加而趨于不穩(wěn)定。所以在非線(xiàn)性控制領(lǐng)域內(nèi)針對(duì)采樣后系統(tǒng)能否穩(wěn)定,以及性能如何,就成了一個(gè)必要的研究課題。
本文在所設(shè)計(jì)的連續(xù)同步控制器的基礎(chǔ)上,基于采樣系統(tǒng)半局實(shí)用漸近穩(wěn)定理論法,對(duì)連續(xù)同步控制器進(jìn)行了再設(shè)計(jì),仿真結(jié)果表明所設(shè)計(jì)的采樣同步控制器與由連續(xù)同步控制器直接離散化所得的控制器相比,具有更快的收斂速度和更寬的采樣周期選擇范圍,這樣就為控制器算法的實(shí)現(xiàn)爭(zhēng)取到更多的運(yùn)算時(shí)間。
2連續(xù)時(shí)間控制器設(shè)計(jì)
以Rossler系統(tǒng)作為響應(yīng)系統(tǒng),把同步控制器加在其第3個(gè)方程中,此時(shí)系統(tǒng)的動(dòng)力學(xué)方程描述為
以Coullet系統(tǒng)為且標(biāo)系統(tǒng),其方程如下:
當(dāng)參數(shù)a1=0 2,b1=0 2,c1= 5.7,a2=-0. 45,b2=1.1,c2=0.8時(shí),兩系統(tǒng)都處于混沌狀態(tài):定義誤差變量:
對(duì)式(4)求一階導(dǎo)數(shù)后帶入式(1),可得
為了便于采用backstepp/ng方法進(jìn)行設(shè)計(jì)(需要嚴(yán)格下三角結(jié)構(gòu)),首先交換上式中e1和e2的下標(biāo),再互換第一個(gè)方程與第二個(gè)方程的位置,令:
則誤差系統(tǒng)狀態(tài)方程式(5)可改寫(xiě)為
此時(shí)只要選取合適的控制輸入u使系統(tǒng)(7)的誤差變量e1(i=1,2,3)全部收斂到零,就能實(shí)現(xiàn)系統(tǒng)(1)與系統(tǒng)(2)的同步。以下將嘗試使用back stepping方法逐少求取同步控制器u。
考慮(e1)子系統(tǒng),把e2當(dāng)成子系統(tǒng)e1的虛擬控制器,令w1=e1選取第一個(gè)Lyapunov函數(shù): 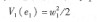 則v1(e1)沿著(e1)子系統(tǒng)的時(shí)間導(dǎo)數(shù)V1(e1)=eiei =el(e2 +aie, +A),令w2=e2- al,并且α=-k1el -alel -A,則v1(e1)= -k1w1 2 +w2e1。其中,k1為選定的正常數(shù),下文也是這樣。 接下來(lái)考慮(e1,e2)子系統(tǒng),把e3當(dāng)作其虛擬控制器,選取第2個(gè)Lyapunov函數(shù):
則V2(e1,e2)沿(e1,e2)子系統(tǒng)的時(shí)間導(dǎo)數(shù):
最后考慮系統(tǒng)(e1,e2,e3),選取:
則V3(e1,e2,e3)的時(shí)間導(dǎo)數(shù):
如果選取:
為了使e2和e3隨時(shí)間t也能收斂于0。實(shí)現(xiàn)Coullet系統(tǒng)與Rissler系統(tǒng)3個(gè)狀態(tài)的完全同步,可在控制期設(shè)計(jì)前先對(duì)響應(yīng)系統(tǒng)盡享補(bǔ)償控制,使補(bǔ)償后的誤差系統(tǒng)不含A,B項(xiàng),選取:
則補(bǔ)償后的響應(yīng)系統(tǒng)為
依然沿用式(3)定義的誤差變量,對(duì)這些變量求一階導(dǎo)數(shù)后帶入式(11)中,可得:
依照前面的方法交換式(12)中的e1和e2的下表并互換第一個(gè)方程與第二個(gè)方程的位置,然后按照backsteping方法對(duì)系統(tǒng)(12)重新進(jìn)行控制器設(shè)計(jì),于是得到
最后再交換會(huì)e1和e2的下表,得:
3采樣控制器設(shè)計(jì)
考慮如下系統(tǒng):
假設(shè)f (O)=0且f和g連續(xù)可微。采樣控制系統(tǒng)中控制信號(hào)U(t)=u(KT)=u(k),為分段連續(xù)信號(hào),狀態(tài)變量η(k)=η(kT)和ξ(k)=ξ(KT)分別可以在采樣時(shí)刻kT被測(cè)量,其中,T>O為采樣周期,非線(xiàn)性系統(tǒng)(14)所對(duì)應(yīng)的精確離散模型和Euler近似離散模型分別表示為
大多情況下,系統(tǒng)( 17)對(duì)應(yīng)的精確離散模型是不可得的,即使可得往往也不能保持如式(17)的嚴(yán)格反饋結(jié)構(gòu),而Euler近似離散模型不但易求,且能夠保持模型的嚴(yán)格反饋結(jié)構(gòu),這是在以下的設(shè)計(jì)中選用非線(xiàn)性系統(tǒng)Euler近似離散模型的原因。
對(duì)離散系統(tǒng)模型:
有以下2個(gè)定義:
定義1 稱(chēng)系統(tǒng)(21)是半局實(shí)用漸近穩(wěn)定( SPAS)的,如果存在函數(shù)βEKl,對(duì)于任意正實(shí)數(shù)對(duì)(Δ,δ),都有 T>0使對(duì)所有和初始狀態(tài)系統(tǒng)(18)的解都滿(mǎn)足.
由定義l可以直接得出,如果系統(tǒng)式(21)是全局漸進(jìn)穩(wěn)定的,那么其必定是半局實(shí)用漸近穩(wěn)定。
定義2 稱(chēng)連續(xù)可微函數(shù)V:Rn-,R是系統(tǒng)(21)的半球?qū)嵱脻u近穩(wěn)定Lyapunov函數(shù),如果存在K;使得對(duì)任意正實(shí)數(shù)對(duì),存在L,T >都滿(mǎn)足下面的式子:
定理l如果(Vt,ut) ,那么ur也可以使FTSPAS。
下面將進(jìn)行采樣同步控制器設(shè)計(jì),首先交換誤差系統(tǒng)(12)中變量ei和e:的下標(biāo),然后求出其Euler近似離散模型:
令
則式(23)可以改寫(xiě)為:
根據(jù)文獻(xiàn){8}中訂立2可以求出能夠使系統(tǒng)式(16)半球?qū)嵱脻u近穩(wěn)定的一個(gè)SPAS對(duì)(V(K),v(K)),其中:
所以(V(K),v(K))是我差系統(tǒng)的Euler近似離散形式(14)的一個(gè)SPAS對(duì),由定理q可知,所求的V(K)同樣可以使得系統(tǒng)式精確離散模型保持半球?qū)嵱脻u近穩(wěn)定。
再把所得控制器v(K)代到(24)中,然后再次交換e1和e2的下表,可得最終的采樣西戎同步控制器表達(dá)式為:
通過(guò)比較U3(K),可知:
通過(guò)計(jì)算可以得出:
由此可以看出,所設(shè)計(jì)的采樣控制器u(k)比直接把連續(xù)控制器離散化所得到的控制器具有更快的收斂速度。
4仿真試驗(yàn)
目標(biāo)Coullet系統(tǒng)在相圖中的混沌吸引子,如圖1所示。
當(dāng)加入連續(xù)時(shí)間同步控制器(u1,u2,u3)后,則響應(yīng)系統(tǒng)同步誤差e(t)=(e12(t)+ e22 (t)+ e32 (t))隨時(shí)間t快速收斂到0,如圖2所示。
這表明在控制器(u1,u2,u3)作用下兩系統(tǒng)間所有狀態(tài)均保持了同步。設(shè)定采樣周期為O l s,兩種采樣控制器同步誤差比較,如圖3所示。
采樣系統(tǒng)往往隨著采樣周期的增加而趨于不穩(wěn)定,當(dāng)T=0. 35 s時(shí),控制器已經(jīng)不能使系統(tǒng)穩(wěn)定,此時(shí)的系統(tǒng)誤差e(t)如圖4所示。
而在控制器作用下,響應(yīng)系統(tǒng)仍能在一定誤差范圍與目標(biāo)系統(tǒng)保持同步,誤差e(t)隨時(shí)間變化曲線(xiàn),如圖5所示。
5結(jié)語(yǔ)
本文以Coullet系統(tǒng)為目標(biāo)系統(tǒng),以Rossler系統(tǒng)為響應(yīng)系統(tǒng),分別設(shè)計(jì)了連續(xù)控制器和采樣控制器來(lái)實(shí)現(xiàn)兩系統(tǒng)之間的全狀態(tài)同步,并進(jìn)一步比較了所設(shè)計(jì)的采樣控制器與由連續(xù)控制器直接離散化所得的控制器之間的性能,仿真結(jié)果證明了所設(shè)計(jì)控制器的優(yōu)越性。

|