直接轉矩控制系統(tǒng)的兩種速度估計器比較研究
姬宣德,蔣建虎
(洛陽理工學院電氣工程與自動化系,洛陽471023)
摘要:采用全階磁鏈閉環(huán)觀測器以實現(xiàn)直接轉矩控制系統(tǒng)定子磁鏈的準確觀測。在此基礎上推導了兩種速度估計器,并對上述兩種速度估計器對比仿真和實驗。仿真和實驗結果表明:依據(jù)模型參考自適應理論設計出的速度估計器比依據(jù)李亞普諾夫理論構造的速度估計器辨識速度收斂快,動態(tài)性能更好。
關鍵詞:交流感應電動機;直接轉矩控制;速度估計囂;模型參考自適應
中圖分類號:TP271 文獻標志碼:A 文章編號:1001-6848{2010)02-0066-04
O引 言
為了滿足高性能交流傳動的需要,需要對速度進行閉環(huán)控制,而速度傳感器的安裝增加了系統(tǒng)的復雜性,降低了系統(tǒng)的可靠性和系統(tǒng)的魯棒性,并增加了系統(tǒng)成本和維護要求。因此,栗用無速度傳感器已經是未來交流調速發(fā)展的必然趨勢。在直接轉矩控制系統(tǒng)中,利用全階磁鏈閉環(huán)觀測器取代傳統(tǒng)的積分器以提高了對定子磁鏈的觀測精度,同時增加對電機參數(shù)的魯棒性。在全階磁鏈閉環(huán)觀測器的基礎上,設計了兩種速度估計器:一種是依據(jù)李亞普諾夫理論設計出的速度估計觀測器;第二種是依據(jù)模型參考自適應理論設計出的速度自適應觀測器。利用MATLAB對兩種速度估計的直接轉矩控制系統(tǒng)進行了仿真實現(xiàn),同時又進行實驗,并對實驗和仿真結果進行了對比分析。
1 直接轉矩控制系統(tǒng)全階磁鏈閉環(huán)觀測器的動態(tài)數(shù)學模型
1。1異步電動機在兩相靜止坐標系下的動態(tài)數(shù)學模型
以定、轉子磁鏈為狀態(tài)變量的矩陣形式電動機數(shù)學模型如下:
電磁轉矩表示為:
1. 2全階磁鏈閉環(huán)觀測器的動態(tài)數(shù)學模型
通過式(1)、式(2)所描述的異步電動機矩陣形式電機數(shù)學模型一狀態(tài)方程,可以構造出同時觀測定子磁鏈和定子電流的全階磁鏈狀態(tài)觀測器[4]:
這里,
上述表達式中,代表觀測器的估計值。U是狀態(tài)觀測器的輸入,輸出是is,K置是觀測器增益矩陣。觀測器的最后一項是包含觀測電流輸出與電機真實電流輸出的修正項。增益矩陣K起到加權矩陣的作用,用于修正觀測所得的定、轉子磁鏈狀態(tài)變量。當觀測器模型使用的矩陣A和實際系統(tǒng)的矩陣A之間存在差異時,必然會導致觀測器輸出與實際輸出之間存在偏差,在此情況下,該附加的修正項將進一步校正這些影響。上式中觀測增益矩陣置可以表示為如下矩陣形式:
2兩種速度估計器
2.1基于李亞普諾夫理論的速度估計器
轉速ωτ是機械變化量,當機械轉速ωτ變化遠遠低于電量變化的速度時,可以將機械轉速ωτ視作常數(shù)。據(jù)此,根據(jù)李亞普諾夫理論推導出轉速ωτ自適應收斂率,并使系統(tǒng)保持穩(wěn)定。
圖1為基于李亞普諾夫理論的速度估計器系統(tǒng)框圖。考慮到估計轉速與實際轉速之間存在的偏差,定、轉子磁鏈實際值與估算值之間的動態(tài)誤差方程可以通過電動機狀態(tài)方程與全階磁鏈狀態(tài)觀測器的差值,即式(1)減去式(4)計算得到:
AA為誤差矩陣:
圖l基于李亞普諾夫理論速度估計器系統(tǒng)框圖定義李亞普諾夫函數(shù)如下:
這里λ是任一正常數(shù),而且
通過求李亞普諾夫函數(shù)(9)對時間的微分運算,且認為未知參數(shù)轉速ωτ變化緩慢,近似為常數(shù),可得:
經過推導可得,上式中:
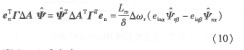
那么,上式變?yōu)?/DIV>
則可以得到電機轉速的自適應收斂率:
由于矩陣j1是非奇異矩陣,那么矩陣I(A -KC)T和(A-KC)的特征值是相同的,因此如果選擇合適的觀測器增益矩陣K,使得矩陣(A-KC)滿足負半定的條件,則按上述的自適應率所構成的速度估計器將是穩(wěn)定的。
因此,采用式(11)作為自適應率,可以使系統(tǒng)保持穩(wěn)定。為了滿足系統(tǒng)的動態(tài)性能的要求,可以采用式(12)所示的比例積分形式的速度自適應率:
上式中,Kp、Ki分別是比例和積分系數(shù)。
2.2基于模型參考自適應理論的速度估計器
圖2是采用模型參考自適應( MRAS)理論設計的另一種自適應速度估計器。將電機的實際模型作為參考模型,同時將前面設計的全階磁鏈狀態(tài)觀測器用作可調模型,那么估算轉速。與實際轉速,的偏差必然會導致兩個模型的輸出電流的偏差。據(jù)此,電機估算轉速CO,的自適應率可以根據(jù)上述兩個模型的輸出電流的偏差得到,即:
上式中:Kp、K1分別是比例和積分系數(shù)。式(14)所示描述的轉速自適應收斂可以采用前面類似的方法通過波渡夫超穩(wěn)定性理論加以證明。
通常,轉速ωτ是變量,式(1)所描述的電機模型是線性時變系統(tǒng)。然而當轉速m,的變化速度遠遠低于電量的變化速度時,可以認為常數(shù)。電機的定子電阻Rs和轉子電阻Rτ隨溫度緩慢變化,也可以看作常數(shù)。據(jù)此,依據(jù)波波夫超穩(wěn)定理論推導出轉速ωτ的新型自適應收斂率,并使系統(tǒng)保持穩(wěn)定狀態(tài)。
辨識轉速與實際轉速之間的偏差必然導致定、轉子磁鏈的估算值與實際值之間的誤差,那么它們的動態(tài)誤差方程可以通過參考模型與可調模型的差值,即式(1)減去式(4)計算得到:
這里,W是非線性時變通道,即
這里Δωτ為實際轉速與估計轉速的偏差,式(15)描述的系統(tǒng)誤差結構可以表示為圖3的形式。系統(tǒng)由線性定常的前饋通道和非線性的反饋通道共同構成,φ(e)為轉速ωτ的自適應辨識率。誤差系統(tǒng)漸進穩(wěn)定的條件是:系統(tǒng)的前饋通道是嚴格正實的,并且非線性反饋通道的輸入和輸出滿足波波夫穩(wěn)定的條件,即:
對于非線性反饋通道,可以證明前饋通道矩陣 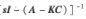 是嚴格正實的,這里不等式(17)可以進一步推導如下: 根據(jù)下面的不等式:
可以知道若采用式(21)所示的轉速的辨識率,可以使式(19)滿足波波夫定理。
這里,X為任意常數(shù)。采用式(21)作為ωτ的自適應率,可以使系統(tǒng)滿足穩(wěn)定條件。為了滿足動態(tài)性能的要求,積分形式的轉速自適應率(21)可以改用式(22)所示的比例積分形式的自適應率[6]:
將上述自適應速度觀測器與全階磁鏈閉環(huán)觀測器結合在一起便構成了第二種速度自適應觀測器(如圖4)。
3仿真和實驗結果分析
從速度估計器的動態(tài)響應仿真波形(圖5和圖6來看,基于李亞普諾夫理論速度估計器的辨識轉速最快也需要20 ms跟蹤并收斂至真實轉速,而基于模型參考自適應速度估計器的辨識轉速幾乎同時跟蹤并收斂至真實轉速;從速度估計器的動態(tài)響應實驗波形(圖7和圖8)來看,基于模型參考自適應速度估計器的辨識轉速也比基于李亞普諾夫理淪速度估計器的辨識轉速收斂快;仿真結果和實驗結果一致。因此,由仿真和實驗結果可知:采用基于模型參考自適應速度估計器所構成的無速度傳感器直接轉矩控制系統(tǒng)與采用基于李亞普諾夫理論速度估計器構成的相應系統(tǒng)相比,辨識速度收斂快,動態(tài)性能更好。
|